题目内容
已知顶点在坐标原点,焦点在x轴上的抛物线被直线y=2x+1截得的弦长为
,求此抛物线方程.
| 15 |
分析:设出抛物线的方程,直线与抛物线方程联立消去y,进而根据韦达定理求得x1+x2的值,进而利用弦长公式求得|AB|,由AB=
可求p,则抛物线方程可得.
| 15 |
解答:解:由题意可设抛物线的方程y2=2px(p≠0),直线与抛物线交与A(x1,y1),B(x2,y2)
联立方程
可得,4x2+(4-2p)x+1=0
则x1+x2=
p-1,x1x2=
,y1-y2=2(x1-x2)
AB=
=
=
=
=
解得p=6或p=-2
∴抛物线的方程为y2=12x或y2=-4x
联立方程
|
则x1+x2=
| 1 |
| 2 |
| 1 |
| 4 |
AB=
| (x1-x2)2+(y1-y2)2 |
| 5(x1-x2)2 |
| 5[(x1+x2)2-4x1x2 ] |
5(
|
| 15 |
解得p=6或p=-2
∴抛物线的方程为y2=12x或y2=-4x
点评:本题主要考查了抛物线的标准方程.解题的关键是对抛物线基本性质和标准方程的熟练应用

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 轴正半轴的抛物线上有一点
轴正半轴的抛物线上有一点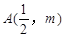 ,
, 点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设
点到抛物线焦点的距离为1.(1)求该抛物线的方程;(2)设 为抛物线上的一个定点,过
为抛物线上的一个定点,过 作抛物线的两条互相垂直的弦
作抛物线的两条互相垂直的弦 ,
, ,求证:
,求证: 恒过定点
恒过定点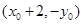 .(3)直线
.(3)直线 与抛物线交于
与抛物线交于 ,
, 两点,在抛物线上是否存在点
两点,在抛物线上是否存在点 ,使得△
,使得△ 为以
为以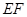 为斜边的直角三角形.
为斜边的直角三角形.