Question

已知顶点在坐标原点的抛物线C的准线方程为y=-1，在[-1，1]上任取两个数a，b，那么点（a，b）在抛物线C上方的概率为

11

24

．

Answer 1

分析：根据准线方程可求得p，注意焦点的位置，则抛物线的标准方程可得．在[-1，1]上任取两个数a，b，故

-1≤a≤1 -1≤b≤1

①，点（a，b）在抛物线C上方，则△=a²-4b＜0②，转化为②和①对应的面积之比即可．

解答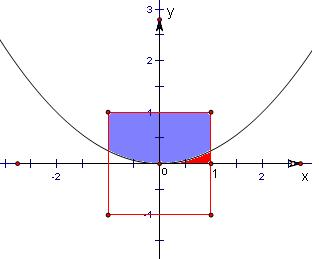：解：∵准线方程y=-1，∴

p

2

=1，解得p=2，
又知抛物线的焦点在y轴上，
故抛物线的方程为x²=4y，
在[-1，1]上任取两个数a，b，故

-1≤a≤1 -1≤b≤1

①，
点（a，b）在抛物线C上方，则a²-4b＜0②
如图：
故点（a，b）在抛物线C上方的概率为阴影部分的面积和①所对应的正方形的面积之比．
红色阴影部分的面积为

∫

1 0

1

4

x2dx=

1

12

x³

|

1 0

=

1

12

，
所以点（a，b）在抛物线C上方的概率为

2-2× 1 12

4

=

11

24

．
故答案为：

11

24

．

点评：本题考查几何概型、定积分的应用等知识．几何概型是新课标新增内容，因此也是考试的热点，而且往往与函数有关知识相结合