题目内容
12.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)过点P(1,$\frac{\sqrt{6}}{2}$),且c=$\sqrt{2}$,定点A的坐标为(1,0).(1)求椭圆C的方程;
(2)若Q为C上的动点,求QA的最大值.
分析 (1)由题意得$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{3}{2{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=2}\end{array}\right.$,从而解得.
(2)利用参数法设Q(2cosθ,$\sqrt{2}$sinθ),从而可得|AQ|=$\sqrt{(2cosθ-1)^{2}+(\sqrt{2}sinθ)^{2}}$,从而解得.
解答  解:(1)由题意得,
解:(1)由题意得,
$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{3}{2{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=2}\end{array}\right.$,
解得,b2=2,a2=4,
故椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(2)设Q(2cosθ,$\sqrt{2}$sinθ),
则|AQ|=$\sqrt{(2cosθ-1)^{2}+(\sqrt{2}sinθ)^{2}}$
=$\sqrt{2(cosθ-1)^{2}+1}$,
故当cosθ=-1,即点Q(-2,0)时,
|AQ|max=3.
点评 本题考查了圆锥曲线的应用及参数法的应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目
20.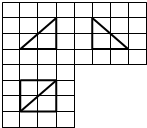 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
 如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )
如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为( )| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
1.设F是椭圆E:$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$的左焦点,过点F且倾斜角为150°的直线l交椭圆E于M,N两点,连接MO(O为坐标原点)并延长交椭圆于P,则△MNP面积为( )
| A. | $\frac{5}{2}$ | B. | 5 | C. | $\frac{15}{2}$ | D. | 10 |
 如图1,已知ABCD是上、下底边长分别为2和6的等腰梯形.将它沿对称轴OO1折成直二面角,如图2,满足AC⊥BO1.
如图1,已知ABCD是上、下底边长分别为2和6的等腰梯形.将它沿对称轴OO1折成直二面角,如图2,满足AC⊥BO1.