题目内容
已知二次函数![]() 同时满足:①不等式
同时满足:①不等式![]() 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在![]() ,使得不等式
,使得不等式![]() 成立。设数列
成立。设数列![]() 的前n项和
的前n项和![]() 。
。
(1)求函数![]() 的表达式;
的表达式;
(2)求数列![]() 的通项公式;
的通项公式;
(3)设各项均不为零的数列![]() 中,所有满足
中,所有满足![]() 的整数i的个数称为这个数列
的整数i的个数称为这个数列![]() 的变号数。令
的变号数。令![]() (n为正整数),求数列
(n为正整数),求数列![]() 的变号数。
的变号数。
解:(1)![]() 的解集有且只有一个元素,
的解集有且只有一个元素,
![]()
当a=4时,函数![]() 上递减,
上递减,
故存在![]() ,使得不等式
,使得不等式![]() 成立
成立
当a=0时,函数![]() 上递增
上递增
故不存在![]() ,使得不等式
,使得不等式![]() 成立
成立
综上,得a=4,![]()
(2)由(1)可知![]()
当n=1时,![]()
当![]() 时,
时,
![]()
![]()
![]()
![]()
(3)由题设 ,
,
![]()
![]()
![]() 递增,
递增,
![]()
即![]() 时,有且只有1个变号数;
时,有且只有1个变号数;
又![]()
∴此处变号数有2个。
综上得数列![]() 的变号数为3。
的变号数为3。

练习册系列答案
相关题目
 同时满足:
同时满足: 的解集有且只有一个元素;
的解集有且只有一个元素; ,使得不等式
,使得不等式 成立.
成立. 的通项公式为
的通项公式为 .
. 的表达式;
的表达式;  项和
项和 .
. 同时满足:①不等式
同时满足:①不等式 的解集有且只有一个元素;②在定义域内存在
的解集有且只有一个元素;②在定义域内存在 ,使得不等式
,使得不等式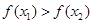 成立,设数列
成立,设数列 的前
的前 项和
项和 。
。 的表达式;
的表达式; 的数列
的数列 中,所有满足
中,所有满足 的整数
的整数 的个数称为这个数列
的个数称为这个数列 (
(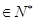 ),求数列
),求数列