Question

已知定义在区间[-p，]   上的函数y=f(x)的图象关于直线x= -对称，当xÎ[-，]时，函数f(x)=Asin(wx+j)(A>0, w>0,-<j<)，其图象如图所示。

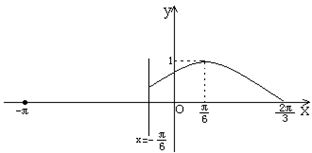(1)求函数y=f(x)在[-p，]的表达式；

(2)求方程f(x)=的解。

Answer 1

解析：(1)由图象知A=1，T=4()=2p，w=

    在xÎ[-，]时

    将(，1)代入f(x)得

    f()=sin(+j)=1

∵-<j<    

∴j=

∴在[-，]时

    f(x)=sin(x+)

    ∴y=f(x)关于直线x=-对称

    ∴在[-p，-]时

    f(x)=-sinx

综上f(x)= 

(2)f(x)=

  在区间[-，]内

可得x₁=    x₂= -

∵y=f(x)关于x= - 对称

∴x₃=-  x₄= -

∴f(x)=的解为xÎ{-,-,-,}