题目内容
椭圆
+y2=1的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使点A1在平面B1A2B2上的射影恰是该椭圆的一个焦点,则此二面角的大小为( )
| x2 |
| 4 |
| A.30 | B.45 | C.60 | D.arctan2 |
由题意画出满足条件的图象如下图所示:
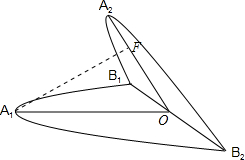
由图可得∠FOA1即为所求二面角的平面角
∵椭圆的标准方程为
+y2=1,
则OA1=2,OF=
∴cos∠FOA1=
=
∴∠FOA1=30°
故选A

由图可得∠FOA1即为所求二面角的平面角
∵椭圆的标准方程为
| x2 |
| 4 |
则OA1=2,OF=
| 3 |
∴cos∠FOA1=
| OF |
| OA1 |
| ||
| 2 |
∴∠FOA1=30°
故选A

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
椭圆
+y2=1的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则P到F2的距离为( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
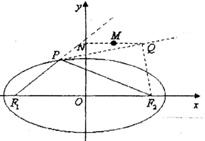 如图,已知椭圆
如图,已知椭圆