题目内容
已知数列{an}的首项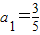 ,an+1=
,an+1=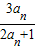 ,n=1,2,….
,n=1,2,….(Ⅰ)求{an}的通项公式;
(Ⅱ)证明:对任意的x>0,
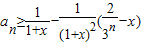 ,n=1,2,….
,n=1,2,….
【答案】分析:(Ⅰ)由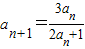 ,知
,知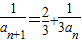 ,故
,故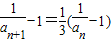 ,由此能够求出{an}的通项公式.(Ⅱ)由
,由此能够求出{an}的通项公式.(Ⅱ)由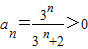 ,知
,知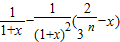 =-
=-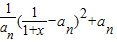 ,由此能够证明对任意的x>0,
,由此能够证明对任意的x>0,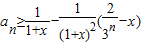 ,n=1,2,…..
,n=1,2,…..
解答:(Ⅰ)解:∵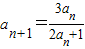 ,
,
∴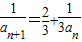 ,
,
∴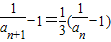 ,
,
又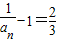 ,
,
∴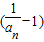 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
∴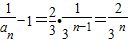 ,
,
∴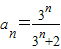 .
.
(Ⅱ)证明:由(Ⅰ)知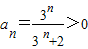 ,
,
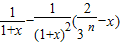
=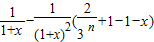
=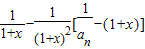
=-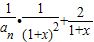
=-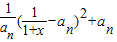
≤an,
∴对任意的x>0,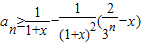 ,n=1,2,….
,n=1,2,….
点评:本题考查数列的递推公式的应用,具体涉及到数列的通项公式的求法和数列与不等式的应用.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答.
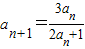 ,知
,知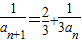 ,故
,故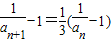 ,由此能够求出{an}的通项公式.(Ⅱ)由
,由此能够求出{an}的通项公式.(Ⅱ)由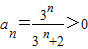 ,知
,知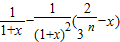 =-
=-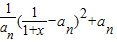 ,由此能够证明对任意的x>0,
,由此能够证明对任意的x>0,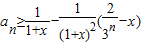 ,n=1,2,…..
,n=1,2,…..解答:(Ⅰ)解:∵
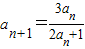 ,
,∴
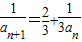 ,
,∴
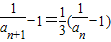 ,
,又
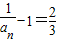 ,
,∴
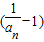 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列. ∴
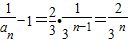 ,
,∴
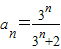 .
.(Ⅱ)证明:由(Ⅰ)知
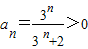 ,
,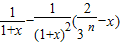
=
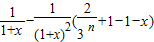
=
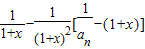
=-
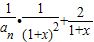
=-
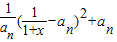
≤an,
∴对任意的x>0,
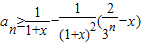 ,n=1,2,….
,n=1,2,….点评:本题考查数列的递推公式的应用,具体涉及到数列的通项公式的求法和数列与不等式的应用.考查运算求解能力,推理论证能力;考查化归与转化思想.解题时要认真审题,仔细解答.

练习册系列答案
相关题目