题目内容
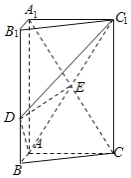
【题目】如图,三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() .
.
(1)试用空间向量证明直线![]() 与平面
与平面![]() 不平行;
不平行;
(2)设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)在(2)的条件下,设平面![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 的所成角.
的所成角.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
可建立空间直角坐标系![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)由![]() 平面
平面![]() 可知
可知![]() ,0,
,0,![]() ,为平面
,为平面![]() 的一个法向量,
的一个法向量,![]() ,
,![]() 即可判定;
即可判定;
(2)求出平面![]() 的法向量,利用平面
的法向量,利用平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,
,![]() ,建立方程,即可求得结论.
,建立方程,即可求得结论.
(3)在(2)的条件下,求出直线![]() 的方向向量,平面
的方向向量,平面![]() 的一个法向量,代入向量夹角公式,可得答案.
的一个法向量,代入向量夹角公式,可得答案.
解:依题意建立如图所示的空间直角坐标系![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
(1)证明:由![]() 平面
平面![]() ,知
,知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
![]()
所以![]()
即直线![]() 与平面
与平面![]() 不平行
不平行
(2)平面![]() 的法向量
的法向量![]() ,则
,则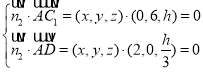
取![]() ,则
,则![]() ,故
,故![]()
所以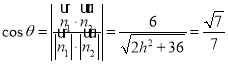
解得![]()
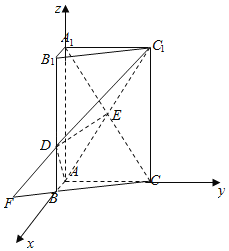
(3)在平面![]() 内,分别延长
内,分别延长![]() ,交于点
,交于点![]() ,连接
,连接![]() ,则直线
,则直线![]() 是平面
是平面![]() 与平面
与平面![]() 交线,
交线,
![]() ,
,![]()
![]()
![]() ,
,
![]() ,
,
![]()
设直线![]() 与平面
与平面![]() 的所成的角是
的所成的角是![]() ,则
,则![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
![]()
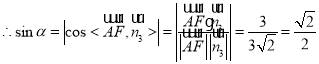
![]()
![]() 直线
直线![]() 与平面
与平面![]() 的所成角为
的所成角为![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】2019年高考刚过,为了解考生对全国2卷数学试卷难度的评价,随机抽取了某学校50名男考生与50名女考生,得到下面的列联表:
非常困难 | 一般 | |
男考生 | 20 | 30 |
女考生 | 40 | 10 |
(1)分别估计该学校男考生、女考生觉得全国2卷数学试卷非常困难的概率;
(2)从该学校随机抽取3名男考生,2名女考生,求恰有4名考生觉得全国2卷数学试卷非常困难的概率.