题目内容
对于定义域为[0，1]的函数f（x），若同时满足以下三个条件：
①f（1）=1；
②
x∈[0，1]，总有f（x）≥0；
③当x1≥0，x2≥0，x1+x2≤1时，都有f（x1+x2）≥f（x1）+f（x2），则称函数f（x）为理想函数．
（Ⅰ）若函数f（x）为理想函数，求f（0）．
（Ⅱ）判断函数g（x）=2x﹣1（x∈[0，1]）和函数 （x∈[0，1]）是否为理想函数？若是，予以证明；若不是，说明理由．
（Ⅲ）设函数f（x）为理想函数，若
x0∈[0，1]，使f（x0）∈[0，1]，且f[f（x0）]=x0，求证：f（x0）=x0．
①f（1）=1；
②
x∈[0，1]，总有f（x）≥0；③当x1≥0，x2≥0，x1+x2≤1时，都有f（x1+x2）≥f（x1）+f（x2），则称函数f（x）为理想函数．
（Ⅰ）若函数f（x）为理想函数，求f（0）．
（Ⅱ）判断函数g（x）=2x﹣1（x∈[0，1]）和函数 （x∈[0，1]）是否为理想函数？若是，予以证明；若不是，说明理由．
（Ⅲ）设函数f（x）为理想函数，若
x0∈[0，1]，使f（x0）∈[0，1]，且f[f（x0）]=x0，求证：f（x0）=x0． 解：（Ⅰ）取x1=x2=0，代入f（x1+x2）≥f（x1）+f（x2），
可得f（0）≥f（0）+f（0）即f（0）≤0
由已知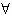
x∈[0，1]，总有f（x）≥0可得f（0）≥0，
∴f（0）=0
（Ⅱ）显然g（x）=2x﹣1在[0，1]上满足g（x）≥0；
②g（1）=1．若x1≥0，x2≥0，且x1+x2≤1，则有
g（x1+x2）﹣[g（x1）+g（x2）]=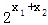 
﹣1﹣[（ 
﹣1）+（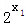 
﹣1）]=（
﹣1）（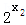 
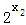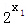﹣1）≥0
故g（x）=2x﹣1满足条件①②③，
所以g（x）=2x﹣1为理想函数．对应函数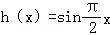 
在x∈[0，1]上满足
①h（1）=1；
②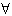
x∈[0，1]，总有h（x）≥0；
③但当x1≥0，x2≥0，x1+x2≤1时，例如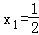 
=x2时，h（x1+x2）=h（1）=1，
而h（x1）+h（x2）=2h（
）=
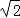，不满足条件③，则函数h（x）不是理想函数．
（Ⅲ）由条件③知，任给m、n∈[0，1]，当m＜n时，由m＜n知n﹣m∈[0，1]，
∴f（n）=f（n﹣m+m）≥f（n﹣m）+f（m）≥f（m）．
若f（x0）＞x0，则f（x0）≤f[f（x0）]=x0，前后矛盾；
若f（x0）＜x0，则f（x0）≥f[f（x0）]=x0，前后矛盾．
故f（x0）=x0．
练习册系列答案
相关题目