题目内容
(本题满分12分)在直三棱柱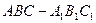 中,
中,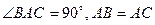 ,直线
,直线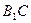 与平面
与平面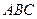 成
成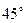 角;
角;

(1)求证:平面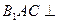 平面
平面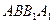 ;
;
(2)求二面角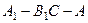 的正弦值.
的正弦值.
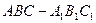 中,
中,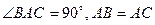 ,直线
,直线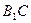 与平面
与平面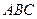 成
成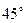 角;
角;
(1)求证:平面
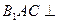 平面
平面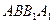 ;
;(2)求二面角
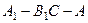 的正弦值.
的正弦值.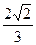
解:(1)证明:由直三棱柱性质得, B1B⊥平面ABC,∴B1B⊥AC,
又BA⊥AC,B1B∩BA=B,∴AC⊥平面 ABB1A1,
又AC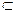 平面B1AC,∴平面B1AC⊥平面ABB1A1……………4分
平面B1AC,∴平面B1AC⊥平面ABB1A1……………4分
(2)过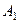 作
作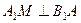 ,垂足为
,垂足为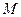 ,过
,过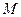 作
作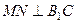 ,垂足为
,垂足为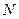 ,连结
,连结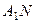 ,…6分
,…6分
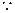 平面
平面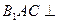 平面
平面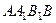 ,且两垂直平面的交线为
,且两垂直平面的交线为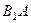 ,
,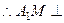 平面
平面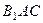 ,
,
由三垂线定理知,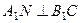 ,
,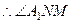 为二面角
为二面角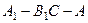 的平面角,……8分
的平面角,……8分
设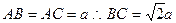 ,
,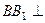 平面
平面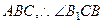 为直线
为直线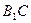 与平面
与平面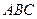
所成的角,故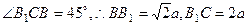 ;
;
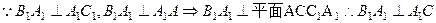
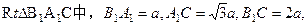
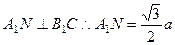
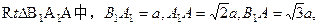
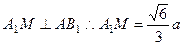
所以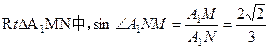
所以二面角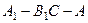 的正弦值为
的正弦值为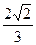 ………………12分.
………………12分.
又BA⊥AC,B1B∩BA=B,∴AC⊥平面 ABB1A1,
又AC
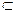 平面B1AC,∴平面B1AC⊥平面ABB1A1……………4分
平面B1AC,∴平面B1AC⊥平面ABB1A1……………4分 (2)过
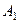 作
作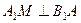 ,垂足为
,垂足为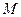 ,过
,过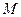 作
作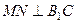 ,垂足为
,垂足为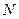 ,连结
,连结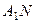 ,…6分
,…6分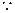 平面
平面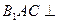 平面
平面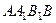 ,且两垂直平面的交线为
,且两垂直平面的交线为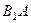 ,
,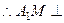 平面
平面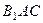 ,
,由三垂线定理知,
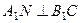 ,
,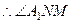 为二面角
为二面角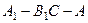 的平面角,……8分
的平面角,……8分设
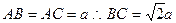 ,
,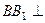 平面
平面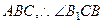 为直线
为直线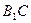 与平面
与平面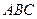
所成的角,故
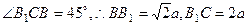 ;
;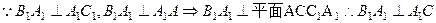
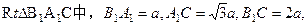
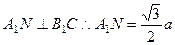
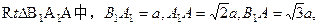
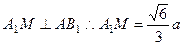
所以
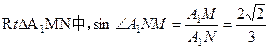
所以二面角
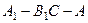 的正弦值为
的正弦值为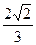 ………………12分.
………………12分.

练习册系列答案
相关题目
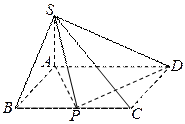 如图,四棱锥
如图,四棱锥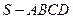 的底面是矩形,
的底面是矩形,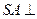 底面
底面 ,P为BC边的中点,SB与
,P为BC边的中点,SB与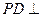 平面SAP;
平面SAP;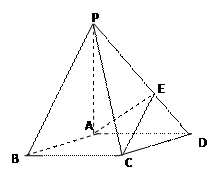 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=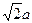 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1. 的大小.
的大小.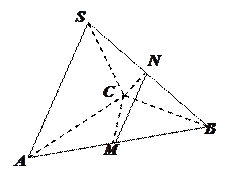 在三棱锥
在三棱锥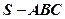 中,
中,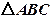 是边长为
是边长为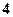 的正三角形,平面
的正三角形,平面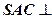 平面
平面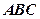 ,
,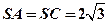 ,
,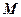 、
、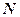 分别为
分别为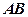 、
、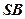 的中点,
的中点,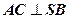 ;
;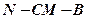 的大小;
的大小;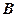 到平面
到平面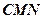 的距离.
的距离. 、
、 、
、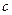 表示三条不同的直线,
表示三条不同的直线,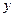 表示平面,给出下列命题:
表示平面,给出下列命题: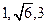 ,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。
,若四面体的四个顶点同在一个球面上,则这个球的表面积为 。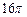 的球面上有三点A、B、C,∠ACB=60°,AB=
的球面上有三点A、B、C,∠ACB=60°,AB=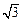 ,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为 ( )
,则球心到截面ABC的距离及B、C两点间球面距离最大值分别为 ( )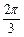
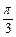

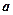 、
、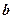 及平面
及平面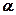 ,给出四个下列命题:
,给出四个下列命题: ,
,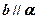 ,则
,则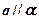 ;
;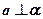 ,
,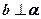 ,则
,则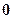 个
个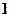 个
个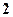 个
个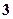 个
个