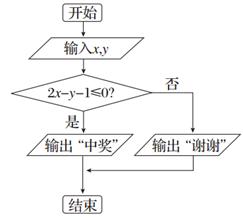
题目内容
袋中装有编号为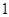 的球
的球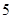 个,编号为
个,编号为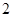 的球
的球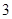 个,这些球的大小完全一样。
个,这些球的大小完全一样。
(1)从中任意取出四个,求剩下的四个球都是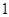 号球的概率;
号球的概率;
(2)从中任意取出三个,记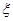 为这三个球的编号之和,求随机变量
为这三个球的编号之和,求随机变量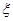 的分布列及其数学期望
的分布列及其数学期望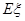 .
.
(1)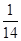 ;(2)分布列见解析,期望为
;(2)分布列见解析,期望为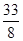
解析试题分析:(1)利用组合的方法求出任意取出四个的所有的方法数,再求出取出的四个中仅有一个1号球的方法数,利用古典概型的概率公式求出剩下的四个球都是1号球的概率.(2)写出随机变量的所有取值,利用古典概型的概率公式求出随机变量取每一个值的概率值,列出分布列,利用随机变量的期望公式求出数学期望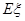 .
.
试题解析:(1)记 “任意取出四个, 剩下的四个球都是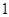 号球”为事件
号球”为事件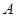 ,
,
则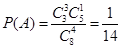 ; (5分)
; (5分)
(2)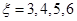
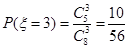 ,
,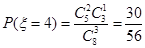 ,
,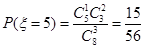 ,
, .
.
所以随机变量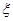 的分布列为
的分布列为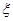
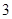
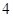
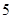
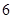
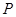

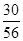
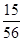
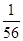
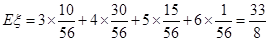 . (14分)
. (14分)
考点:古典概型;离散型随机变量的分布列及其期望

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
已知从全部210人中随机抽取1人为优秀的概率为
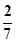 .
.(1)请完成上面的2×2列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”.
附:
 ,其中
,其中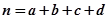 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
我国政府对PM2.5采用如下标准:
| PM2.5日均值m(微克/立方米) | 空气质量等级 |
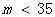 | 一级 |
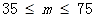 | 二级 |
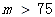 | 超标 |
某市环保局从180天的市区PM2.5监测数据中,随机抽取l0天的数据作为样本,监测值如茎叶图所示(十位为茎,个位为叶).

(1)求这10天数据的中位数.
(2)从这l0天的数据中任取3天的数据,记
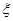 表示空气质量达到一级的天数,求
表示空气质量达到一级的天数,求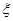 的分布列;
的分布列;(3)以这10天的PM2.5日均值来估计这180天的空气质量情况,其中大约有多少天的空气质量达到一级.
 ,乙出现的点数为
,乙出现的点数为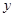 ,若令
,若令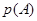 为
为 的概率,
的概率,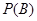 为
为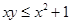 的概率,试求
的概率,试求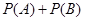 的值.
的值.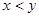 ”
”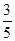 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是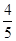 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用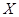 表示张同学答对题的个数,求
表示张同学答对题的个数,求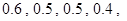 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.