题目内容
A、B是抛物线y2=2px(p＞0)上的两点,且OA⊥OB,求证:直线AB过定点(2p,0).
解析:设A(x1,y1),B(x2,y2),
∵OA⊥OB,∴
=-1,∴x1x2+y1y2=0.
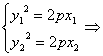x1x2=
,
∴
+y1y2=0.∴y1y2=-4p2.
kAP-kBP=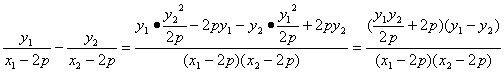
=0.
∴A、B、P三点共线,即直线AB过点P(2p,0).
练习册系列答案
阅读快车系列答案
相关题目
已知A、B是抛物线y2=2px（p＞0）上异于原点O的两点，则“
•
=0”是“直线AB恒过定点（2p，0）”的（ ）
| OA |
| OB |
| A、充分非必要条件 |
| B、充要条件 |
| C、必要非充分条件 |
| D、非充分非必要条件 |
[理]已知A、B是抛物线y2=4x上两点，且
•
=0，则原点O到直线AB的最大距离为（ ）
| OA |
| OB |
| A、2 | B、3 | C、4 | D、8 |