题目内容
设直线x="t" 与函数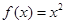 ,
, 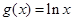 的图像分别交于点M,N,则当
的图像分别交于点M,N,则当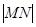 为最小时t的值为
为最小时t的值为
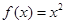 ,
, 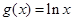 的图像分别交于点M,N,则当
的图像分别交于点M,N,则当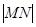 为最小时t的值为
为最小时t的值为| A.1 | B. | C. | D. |
D
解:设函数y=f(x)-g(x)=x2-lnx(x>0),求导数得y′=2x-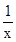 (x>0)
(x>0)
令y′<0,则函数在(0, )上为单调减函数,令y′>0,则函数在(
)上为单调减函数,令y′>0,则函数在( ,+∞)上为单调增函数,
,+∞)上为单调增函数,
所以当x= 时,函数取得最小值为
时,函数取得最小值为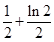 ,所以当MN达到最小时t的值为
,所以当MN达到最小时t的值为 ,选D
,选D
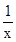 (x>0)
(x>0)令y′<0,则函数在(0,
 )上为单调减函数,令y′>0,则函数在(
)上为单调减函数,令y′>0,则函数在( ,+∞)上为单调增函数,
,+∞)上为单调增函数,所以当x=
 时,函数取得最小值为
时,函数取得最小值为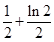 ,所以当MN达到最小时t的值为
,所以当MN达到最小时t的值为 ,选D
,选D
练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
 有三个零点
有三个零点 ,且
,且 则下列结论正确的是( )
则下列结论正确的是( )



 .
. 能否为函数
能否为函数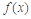 的极值点,并说明理由;
的极值点,并说明理由;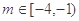 ,使得定义在
,使得定义在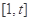 上的函数
上的函数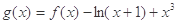 在
在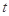 的最大值.
的最大值. 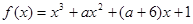 既有极大值又有极小值,则
既有极大值又有极小值,则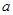 的取值范围为( )
的取值范围为( )



 在
在 及
及 时取得极值.
时取得极值. ,都有
,都有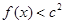 成立,求c的取值范围(6分)
成立,求c的取值范围(6分)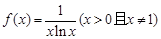 .
.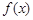 的单调区间;
的单调区间; 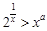 对任意
对任意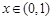 成立,求实数
成立,求实数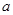 的取值范围;
的取值范围;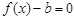 的零点个数.
的零点个数.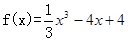 在
在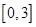 上的最大值是( )
上的最大值是( )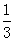
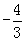
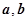 满足:
满足: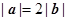 ,若函数
,若函数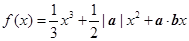 在
在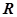 上有极值,设向量
上有极值,设向量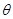 ,则
,则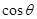 的取值范围为( )
的取值范围为( )
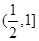


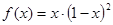 的极值点的个数是( )
的极值点的个数是( )