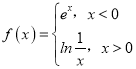Question

【题目】已知函数.

（1）若，解不等式；

（2）关于的不等式有解，求实数的取值范围.

Answer 1

【答案】（1）或；（2）或.

【解析】

通过讨论x的范围，求出不等式的解集即可；（2）令f（x）=|x﹣a|﹣|x﹣3|，依题

意：f（x）max＞2，求出a的范围即可．

（1）当a=1时，原不等式等价于：|x﹣1|+|2x﹣3|＞2．

当x≥时，3x﹣4＞2，解得：x＞2

当1＜x＜时，2﹣x＞2，无解

当x＜1时，4﹣3x＞2，解得：x＜

∴原不等式的解集为：{x|x＞2或x＜}

f（x）＞|x﹣3||x﹣a|﹣|x﹣3|＞1

令f（x）=|x﹣a|﹣|x﹣3|，依题意：f（x）max＞2

∵f（x）=|x﹣a|﹣|x﹣3|≤|a﹣3|，

∴f（x）max=|a﹣3|

∴，解得或 .