题目内容
斜率为2的直线l与双曲线
-
=1交于A，B两点，且|AB|=4，则直线l的方程为
| x2 |
| 3 |
| y2 |
| 2 |
y=2x±
| ||
| 3 |
y=2x±
．
| ||
| 3 |
分析：设出直线方程，代入双曲线方程，利用韦达定理，计算弦长，即可求得结论．
解答：解：设直线的方程为y=2x+b，代入
-
=1，可得10x2+12bx+3b2+6=0
设A，B的横坐标分别为x1，x2，则x1+x2=-
，x1x2=
∵|AB|=4，
∴
•
=4
∴5（
-4•
）=16
∴b=±
∴直线l的方程为y=2x±
故答案为：y=2x±
| x2 |
| 3 |
| y2 |
| 2 |
设A，B的横坐标分别为x1，x2，则x1+x2=-
| 6b |
| 5 |
| 3b2+6 |
| 10 |
∵|AB|=4，
∴
| 1+4 |
| (x1+x2)2-4x1x2 |
∴5（
| 36b2 |
| 25 |
| 3b2+6 |
| 10 |
∴b=±
| ||
| 3 |
∴直线l的方程为y=2x±
| ||
| 3 |
故答案为：y=2x±
| ||
| 3 |
点评：本题考查直线与双曲线的位置关系，考查韦达定理的运用，考查学生的计算能力，属于基础题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
交于A，B两点，且|AB|＝4，求直线的方程．
交于A，B两点，且|AB|＝4，求直线的方程．
-
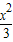=1交于A，B两点，且|AB|=4，则直线l的方程为________．
-
=1交于A，B两点，且|AB|=4，则直线l的方程为 ．