题目内容
已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为其右焦点,
为其右焦点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程及离心率;
的方程及离心率;
(Ⅱ)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当直线
,当直线![]() 绕点
绕点![]() 转动时,试判断以
转动时,试判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
解:(Ⅰ)由题意可设椭圆![]() 的方程为
的方程为![]() ,
,![]() .
.
由题意知
 解得
解得![]() ,
,![]() .
.
故椭圆![]() 的方程为
的方程为![]() ,离心率为
,离心率为![]() .
. ……6分
……6分
(Ⅱ)以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
证明如下:由题意可设直线![]() 的方程为
的方程为![]()
![]() .
.
则点![]() 坐标为
坐标为![]() ,
,![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
所以![]() ,
,![]() . ……………………………10分
. ……………………………10分
因为点![]() 坐标为
坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
直线![]() 轴,此时以
轴,此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离
 .
.
又因为![]() ,所以
,所以![]() .
.
故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当直线![]() 绕点
绕点![]() 转动时,以
转动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.………14分
相切.………14分

练习册系列答案
相关题目
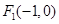 、
、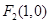 为椭圆
为椭圆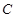 的左、右焦点,且点
的左、右焦点,且点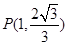 在椭圆
在椭圆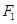 的直线
的直线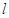 交椭圆
交椭圆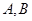 两点,则
两点,则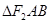 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值?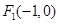 、
、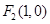 为椭圆
为椭圆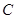 的左、右焦点,且点
的左、右焦点,且点 在椭圆
在椭圆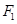 的直线
的直线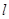 交椭圆
交椭圆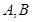 两点,则
两点,则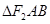 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值? 分别为椭圆
分别为椭圆 的左、右焦点,点
的左、右焦点,点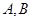 在椭圆上,且
在椭圆上,且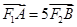
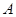 的坐标;
的坐标; 与点
与点 上有一点
上有一点 在
在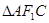 的外接圆上,求
的外接圆上,求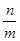 的值
的值 分别为椭圆
分别为椭圆 的左、右顶点,点
的左、右顶点,点 ,直线
,直线 :
: 与
与 轴交于点D,与直线AC交于点P.若
轴交于点D,与直线AC交于点P.若 ,则该椭圆的离心率为( )
,则该椭圆的离心率为( ) B.
B.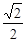 C.
C.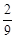 D.
D.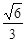
 分别为椭圆
分别为椭圆 的左、右两个焦点,一条直线
的左、右两个焦点,一条直线 经过点
经过点 与椭圆交于
与椭圆交于 两点, 且
两点, 且 的周长为8。
的周长为8。 的值;
的值;
 ,求
,求 的值。
的值。