题目内容
(本题满分16分)
如图,开发商欲对边长为 的正方形
的正方形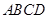 地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路
地段进行市场开发,拟在该地段的一角建设一个景观,需要建一条道路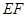 (点
(点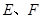 分别在
分别在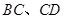 上),根据规划要求
上),根据规划要求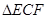 的周长为
的周长为 .
.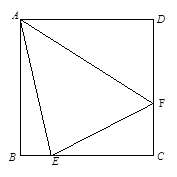
(1)设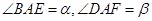 ,求证:
,求证: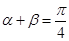 ;
;
(2)欲使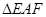 的面积最小,试确定点
的面积最小,试确定点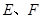 的位置.
的位置.
(1) ,则
,则 ,
,
由已知得: ,
,
 , (2)当
, (2)当 时,
时, 的面积最小.
的面积最小.
解析试题分析:(1)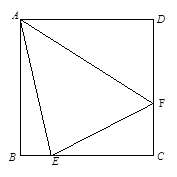
 ,
,
则 ,
,
由已知得: ,
,
即 …………………………4分
…………………………4分
 , …………………………8分
, …………………………8分
(2)由(1)知, 
=
= . …………………………………………………12分
. …………………………………………………12分 ,
, ,即
,即 时
时 的面积最小,最小面积为
的面积最小,最小面积为 .
. ,故此时
,故此时 …………14分
…………14分
所以,当 时,
时, 的面积最小.………………………………16分
的面积最小.………………………………16分
考点:本题考查了三角函数的实际运用
点评:对于三角函数的证明和应用问题,除了要求学生掌握常见的三角变换公式之外,还要掌握三角函数的性质

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
(满分12分)
某市居民生活用水标准如下:
| 用水量t(单位:吨) | 每吨收费标准(单位:元) |
| 不超过2吨部分 | m |
| 超过2吨不超过4吨部分 | 3 |
| 超过4吨部分 | n |
(1)写出y关于t的函数关系式;
(2)某用户希望4月份缴纳的水费不超过18元,求该用户最多可以用多少吨水?
 ,
,
 时,求
时,求 的最大值和最小值
的最大值和最小值 ,求
,求 的取值范围
的取值范围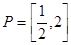 ,函数
,函数 的定义域为
的定义域为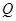
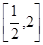 上是增函数,求实数
上是增函数,求实数 的取值范围
的取值范围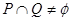 ,求实数
,求实数 的方程
的方程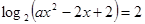 在区间
在区间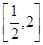 内有解,求实数
内有解,求实数 .
. 为偶函数,求
为偶函数,求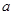 的值;
的值;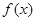 在
在 上有最小值9,求
上有最小值9,求 。
。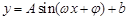 的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为
的图像.2013年1月下旬荆门地区连续几天最高温度都出现在14时,最高温度为 ;最低温度出现在凌晨2时,最低温度为零下
;最低温度出现在凌晨2时,最低温度为零下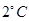 .
.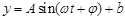
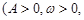
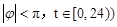 的表达式;
的表达式;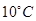 ,教室就要开空调,请问届时学校后勤应该送电吗?
,教室就要开空调,请问届时学校后勤应该送电吗?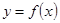 满足:对任意的实数
满足:对任意的实数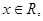 有
有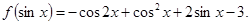
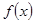 的解析式;
的解析式;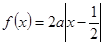 有解,求实数
有解,求实数 的取值范围.
的取值范围.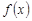 =
=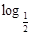 (ex-1)。
(ex-1)。