题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解:f(x)= = = =2sin(2x+ 由2kπ- kπ- ∴f(x)的递增区间为 |
(2) |
解:f(A)=2sin(2A+ ∴sin(2A+ ∴2A+ ∴A= 由余弦定理得a2=b2+c2-2bccosA 3=9+c2―3 (c-2 ∴c=2 |

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 (m,n
(m,n N*),且m>n≥1,若
N*),且m>n≥1,若 ,
, ,且
,且 ,求证:
,求证: .
. 相等?若存在,求x的值;若不存在,请说明理由.
相等?若存在,求x的值;若不存在,请说明理由.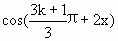 +
+ (k∈Z)
(k∈Z)