题目内容
已知两定点A(2,5),B(-2,1),M和N是过原点的直线l上的两个动点,且|MN|=2
,l∥AB,如果直线AM和BN的交点C在y轴上;
(Ⅰ)求M,N与C点的坐标;
(Ⅱ)求C点到直线l的距离.
| 2 |
(Ⅰ)求M,N与C点的坐标;
(Ⅱ)求C点到直线l的距离.
(Ⅰ) 直线l的斜率即AB的斜率,为
=1,故过原点的直线l 的方程为 y=x.
设M(a,a),则N(a+2,a+2),设C(0,b),由A、C、M三点共线可得
=
①.
由B、C、N 三点共线可得
=
②.
由①②解得 a=-1,b=1,∴M(-1,-1),N(1,1),C (0,1).
(Ⅱ)由两点式求得AB的方程为
=
,即 x-y+3=0,故C点到直线l的距离为
=
.
| 5-1 |
| 2+2 |
设M(a,a),则N(a+2,a+2),设C(0,b),由A、C、M三点共线可得
| 5-b |
| 2-0 |
| 5-a |
| 2-a |
由B、C、N 三点共线可得
| 1-b |
| -2-0 |
| 1-(a+2) |
| -2-(a+2) |
由①②解得 a=-1,b=1,∴M(-1,-1),N(1,1),C (0,1).
(Ⅱ)由两点式求得AB的方程为
| y-1 |
| 5-1 |
| x+2 |
| 2+2 |
| |0-1+3| | ||
|
| 2 |

练习册系列答案
相关题目
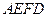 的两条对角线相交于点
的两条对角线相交于点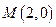 ,
,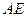 边所在直线的方程为:
边所在直线的方程为: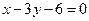 ,点
,点 在
在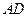 边所在直线上。
边所在直线上。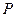 的方程。
的方程。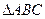 是
是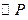 的内接三角形,其重心
的内接三角形,其重心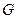 的坐标是
的坐标是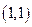 ,求直线
,求直线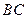 的方程 .
的方程 .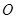 的直径,
的直径,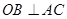 ,弦BN交AC于点M,若
,弦BN交AC于点M,若 ,OM=1,则MN的长为 .
,OM=1,则MN的长为 .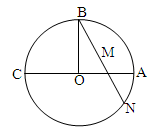
 是圆
是圆 的直径,点
的直径,点 在圆
在圆 到
到 使
使 ,过
,过 于
于 .若
.若 ,
, 则
则 _________.
_________.