题目内容
若一次函数f(x)满足f[f(x)]=x+1,则 的值域为________.
的值域为________.
[2,+∞)
分析:函数f(x)的形式是一次函数,利用待定系数先设出f(x),代入等式f[f(x)]=x+1,解方程求出f(x)得到g(x)的解析式,然后利用基本不等式可求出函数g(x)的值域.
解答:设f(x)=kx+b(k≠0)
∴f[f(x)]
=k(kx+b)+b
=k2x+kb+b
=k2x+(k+1)b…①
依题意:f[f(x)]=1+x…②
∴比较①和②的系数可得:
k2=1…③
(k+1)b=1…④
由③④得:k=1,b= ,k=-1(舍去)
,k=-1(舍去)
∴f(x)=x+
则g(x)= =x+
=x+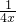 +1≥2
+1≥2 +1=2
+1=2
当且仅当x= 时取等号
时取等号
∴ 的值域为[2,+∞)
的值域为[2,+∞)
故答案为:[2,+∞)
点评:本题主要考查了待定系数法求函数解析式,以及利用基本不等式求函数的值域,同时考查了运算求解的能力,属于中档题.
分析:函数f(x)的形式是一次函数,利用待定系数先设出f(x),代入等式f[f(x)]=x+1,解方程求出f(x)得到g(x)的解析式,然后利用基本不等式可求出函数g(x)的值域.
解答:设f(x)=kx+b(k≠0)
∴f[f(x)]
=k(kx+b)+b
=k2x+kb+b
=k2x+(k+1)b…①
依题意:f[f(x)]=1+x…②
∴比较①和②的系数可得:
k2=1…③
(k+1)b=1…④
由③④得:k=1,b=
 ,k=-1(舍去)
,k=-1(舍去)∴f(x)=x+

则g(x)=
 =x+
=x+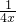 +1≥2
+1≥2 +1=2
+1=2当且仅当x=
 时取等号
时取等号∴
 的值域为[2,+∞)
的值域为[2,+∞)故答案为:[2,+∞)
点评:本题主要考查了待定系数法求函数解析式,以及利用基本不等式求函数的值域,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
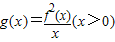 的值域为 .
的值域为 .