题目内容
观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12 ….则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A.76 | B.80 | C.86 | D.92 |
B
解析

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
对于任意正整数n,定义“ ”如下:
”如下:
当n是偶数时, ,
,
当n是奇数时,
现在有如下四个命题:
① ;
;
② ;
;
③ 的个位数是0;
的个位数是0;
④ 的个位数是5。
的个位数是5。
其中正确的命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知 △ABC中,
△ABC中, ,求证:
,求证: .证明:
.证明: ∴
∴ ,其中,画线部分是演绎推理的( )
,其中,画线部分是演绎推理的( )
| A.小前提 | B.大前提 | C.结论 | D.三段论 |
用数学归纳法证明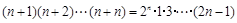 ,从
,从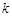 到
到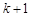 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()
A.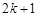 | B.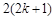 | C.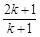 | D.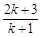 |
下面四个判断中,正确的是( )
| A.式子1+k+k2+…+kn(n∈N*)中,当n=1时式子值为1 |
| B.式子1+k+k2+…+kn-1(n∈N*)中,当n=1时式子值为1+k |
C.式子1+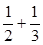 +…+ +…+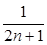 (n∈N*)中,当n=1时式子值为1+ (n∈N*)中,当n=1时式子值为1+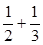 |
D.设f(x)=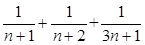 (n∈N*),则f(k+1)=f(k)+ (n∈N*),则f(k+1)=f(k)+ |
设 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且 满足:“当
满足:“当 成立时,总可推出
成立时,总可推出 成立”,那么,下列命题总成立的是 ( )
成立”,那么,下列命题总成立的是 ( )
A.若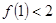 成立,则 成立,则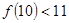 成立 成立 |
B.若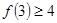 成立,则当 成立,则当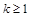 时,均有 时,均有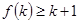 成立 成立 |
C.若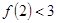 成立,则 成立,则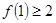 成立 成立 |
D.若 成立,则当 成立,则当 时,均有 时,均有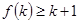 成立 成立 |
分析法是从要证明的结论出发,逐步寻求使结论成立的( )
| A.充分条件 | B.必要条件 | C.充要条件 | D.等价条件 |
用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”的第二步
是( ).
| A.假使n=2k+1时正确,再推n=2k+3正确 |
| B.假使n=2k-1时正确,再推n=2k+1正确 |
| C.假使n=k时正确,再推n=k+1正确 |
| D.假使n≤k(k≥1),再推n=k+2时正确(以上k∈N+) |
 、
、 、
、 、
、 号位上(如图),第一次前后
号位上(如图),第一次前后 这样交替进行下去,那么第
这样交替进行下去,那么第 次互换座位后,小兔坐
次互换座位后,小兔坐