Question

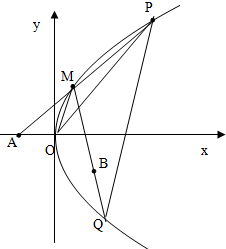已知点A（-1，0），B（1，-1），抛物线C：y²=4x，O为坐标原点，过点A的动直线l交抛物线C于M，P，直线MB交抛物线C于另一点Q．
（I）若向量

OM

与

OP

的夹角为

π

4

，求△POM的面积；
（Ⅱ）证明直线PQ恒过一个定点．

Answer 1

分析：（I）设点p，M，A三点共线进而可知AM和PM的斜率相等求得y₁y₂=4进而根据向量积的运算和两向量的夹角，求得|

OM

|•|

OP

|•cos45°的值，进而利用三角形面积公式求得三角形POM的面积．
（II）设出Q的坐标，根据M，B，Q共线，利用BQ和QM的斜率相等利用点的坐标求得y₁y₃+y₁+y₃+4=0．，把y₁y₂=4代入求得y₂和y₃的关系式，表示出PQ的斜率，进而可表示出直线PQ的方程，进而利用4（y₂+y₃）+y₂y₃+4=0求得（y+4）（y₂+y₃）=4（x-1），进而可推断出直线PQ过定点．

解答：解：（I）设点p，M，A三点共线，∴k_AM=k_PM，
即

y1

y 2 1 4 +1

=

y1-y2

y 2 1 4 - y 2 2 4

，即

y1

y 2 1 +4

=

1

y1+y2

，∴y₁y₂=4，
∴

OM

•

OP

=

y 2 1

4

•

y 2 2

4

+y1y2=5．
∵向量

OM

与

OP

的夹角为45°，∴|

OM

|•|

OP

|•cos45°=5，
∴S△POM=

1

2

|

OM

|•|

OP

|•sin45°=

5

2

．
（II）设点Q(

y 2 3

4

，y₃），
∵M，B，Q三点共线，∴k_BQ=k_QM，
即

y3+1

y 2 3 4 -1

=

y1-y3

y 2 1 4 - y 2 3 4

，即

y3+1

y 2 3 -4

=

1

y1+y3

，
∴（y₃+1）（y₁+y₃）=y₃²-4，即y₁y₃+y₁+y₃+4=0．
∵y₁y₂=4，即y1=

4

y2

，∴

4

y2

•y3+

4

y2

+y3+4=0，
即4（y₂+y₃）+y₂y₃+4=0．（*）∵kPQ=

y2-y3

y 2 2 4 - y 2 3 4

=

4

y2+y3

，
∴直线PQ的方程是y-y2=

4

y2+y3

(x-

y 2 2

4

)，
即（y-y₂）（y₂+y₃）=4x-y₂²，即y（y₂+y₃）-y₂y₃=4x．
由（*）式，-y₂y₃=4（y₂+y₃）+4，代入上式，得（y+4）（y₂+y₃）=4（x-1）．
由此可知直线PQ过定点E（1，-4）．

点评：本题主要考查了抛物线的应用，平面解析几何的基础知识．考查了学生分析推理和基本的运算能力．