题目内容
已知双曲线G的中心在原点,它的渐近线方程是y=±
x.过点P(-4,0)作斜率为
的直线l,使得l和G交于A,B两点,和y轴交于点C,点P在线段AB上,并且满足|PA|•|PB|=|PC|2,求双曲线G的方程.
| 1 |
| 2 |
| 1 |
| 4 |
分析:先根据渐近线方程设出双曲线的方程为x2-4y2=λ,再求出直线l的方程代入双曲线方程,得x1+x2,x1x2,最后将|PA|•|PB|=|PC|2等价为(x1+4)•(x2+4)+y1y2=-17,列方程求出λ即可
解答:解:设所求双曲线方程为(x+2y)(x-2y)=λ,即x2-4y2=λ (λ≠0)
∵直线l点P(-4,0)作斜率为
,∴直线方程为y=
x+1,
设A(x1,y1),B(x2,y2)C(0,1),∴
=(x1+4,y1),
=(x2+4,y2)
联立直线方程与双曲线方程,
,3x2-8x-16-4λ=0
得,x1+x2=
,x1x2=
①
∵|PA|•|PB|=|PC|2,∴
•
=-17
即(x1+4)•(x2+4)+y1y2=-17
即(x1+4)•(x2+4)+(
x1+1)•(
x2+1)=-17
即x1x2+4(x1+x2)=-32 ②
将①代入②解得λ=28
故双曲线方程为x2-4y2=28
∵直线l点P(-4,0)作斜率为
| 1 |
| 4 |
| 1 |
| 4 |
设A(x1,y1),B(x2,y2)C(0,1),∴
| PA |
| PB |
联立直线方程与双曲线方程,
|
得,x1+x2=
| 8 |
| 3 |
| -16-4λ |
| 3 |
∵|PA|•|PB|=|PC|2,∴
| PA |
| PB |
即(x1+4)•(x2+4)+y1y2=-17
即(x1+4)•(x2+4)+(
| 1 |
| 4 |
| 1 |
| 4 |
即x1x2+4(x1+x2)=-32 ②
将①代入②解得λ=28
故双曲线方程为x2-4y2=28
点评:本题考查了双曲线的几何性质,双曲线的标准方程,直线与双曲线的关系等知识,解题时要学会运用待定系数法求标准方程,学会运用韦达定理解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
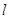 ,使得
,使得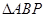 的面积最大时点P的坐标.
的面积最大时点P的坐标.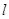 ,使得
,使得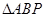 的面积最大时点P的坐标.
的面积最大时点P的坐标.