Question

已知集合A={x||x-1|≤1}，B={x|x²-4ax+3a²≤0，a≥0}
（1）当a=1时，求集合A∩B；
（2）若A∩B=B，求实数a的取值范围．

Answer 1

分析：（1）求出集合A，当a=1时，求出集合B，利用集合交集的定义，即可得到答案；
（2）根据A∩B=B，可得B⊆A，利用子集关系列出不等式组，求解即可求得实数a的取值范围．

解答：解：（1）由|x-1|≤1，即-1≤x-1≤1，
解得0≤x≤2，
∴A=[0，2]，
当a=1时，B={x|x²-4x+3≤0}={x|1≤x≤3}，

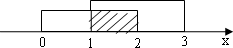
结合数轴，可知A∩B=[1，2]；
（2）∵x²-4ax+3a²≤0，即（x-a）（x-3a）≤0，
又∵a≥0，
∴B={x|a≤x≤3a}
∵A∩B=B，
∴B⊆A，

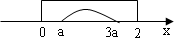
结合数轴可得，

a≥0 3a≤2

，解得a∈[0，

2

3

]，
故实数a的取值范围为a∈[0，

2

3

]．

点评：本题考查了集合的包含关系的判断与应用，集合的交集的运算．考查了含有绝对值不等式的解法，一元二次不等式的解法．对于集合的交并补以及子集关系的元素，一般会借助数轴进行分析求解．属于基础题．