题目内容
解不等式|2x-4|＜4-|x|．分析：根据绝对值的意义，分类讨论，当x＜0时，当0≤x＜2时，当2≤x 时，分别求出不等式的解集，再把这些解集取并集即得原不等式的解集．
解答：解：当x＜0时，不等式即4-2x＜4+x，解得x＞0，故不等式无解．
当0≤x＜2时，不等式即4-2x＜4-x，解得x＞0，故不等式的解集为{x|2＞x＞0}．
当2≤x 时，不等式即2x-4＜4-x，解得x＜
，故不等式的解集为{x|2≤x＜
}．
综上，不等式的解集为{x|2＞x＞0}∪{x|2≤x＜
}={x|
＞x＞0}．
当0≤x＜2时，不等式即4-2x＜4-x，解得x＞0，故不等式的解集为{x|2＞x＞0}．
当2≤x 时，不等式即2x-4＜4-x，解得x＜
| 8 |
| 3 |
| 8 |
| 3 |
综上，不等式的解集为{x|2＞x＞0}∪{x|2≤x＜
| 8 |
| 3 |
| 8 |
| 3 |
点评：本题考查绝对值不等式的解法，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
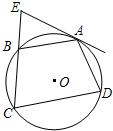A．如图，四边形ABCD内接于⊙O，弧AB=弧AD，过A点的切线交CB的延长线于E点．