题目内容
从{1,3,5,7}中随机选取一个数为m,从{1,2,4}中随机选取一个数为n,则n>m的概率是
- A.

- B.

- C.

- D.

C
分析:从{1,3,5,7}中随机选取一个数为m,从{1,2,4}中随机选取一个数为n,共有4×3=12种情况,而当n>m时,n=2,m=1;n=4,m=1或3,共有3种情况,由古典概型可得答案.
解答:从{1,3,5,7}中随机选取一个数为m,从{1,2,4}中随机选取一个数为n,
由分部计数原理可得:共有4×3=12种情况,
而当n>m时,n=2,m=1;n=4,m=1或3,共有3种情况,
∴n>m的概率是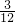 =
=
故选C
点评:本题考查古典概率的求解,解题的关键是确定基本事件的个数,属基础题.
分析:从{1,3,5,7}中随机选取一个数为m,从{1,2,4}中随机选取一个数为n,共有4×3=12种情况,而当n>m时,n=2,m=1;n=4,m=1或3,共有3种情况,由古典概型可得答案.
解答:从{1,3,5,7}中随机选取一个数为m,从{1,2,4}中随机选取一个数为n,
由分部计数原理可得:共有4×3=12种情况,
而当n>m时,n=2,m=1;n=4,m=1或3,共有3种情况,
∴n>m的概率是
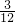 =
=
故选C
点评:本题考查古典概率的求解,解题的关键是确定基本事件的个数,属基础题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目