题目内容
设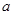 、b是两条不同的直线,
、b是两条不同的直线,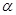 、
、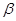 是两个不同的平面,则下列四个命题中正确的是(
)
是两个不同的平面,则下列四个命题中正确的是(
)
A.若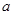 ⊥b,
⊥b,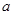 ⊥
⊥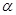 ,则b∥
,则b∥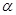 B.若
B.若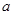 ∥
∥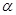 ,
,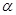 ⊥
⊥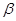 ,则
,则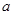 ⊥
⊥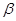
C.若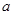 ⊥
⊥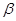 ,
,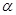 ⊥
⊥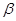 ,则
,则 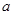 ∥
∥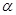 D.若
D.若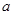 ⊥b,
⊥b,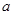 ⊥
⊥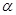 ,b⊥
,b⊥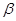 ,则
,则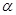 ⊥
⊥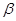
【答案】
D
【解析】
试题分析:空间中的线面位置关系,以及面面位置关系的判定可以借助于长方体来判定,也可以借助于现实中的物体来得到。
选项A中,两条垂直的直线中一条垂直与此平面,另一条可能平行,也可能在平面内,因此错误。
选项B中, ⊥
⊥ ,当
,当 ∥
∥ 时,则直线a可能在平面
时,则直线a可能在平面 内。因此错误
内。因此错误
选项C中,直线a可能在平面 内,因此错误。
内,因此错误。
排除法选D.
考点:本试题主要是考查了线面平行和面面垂直,以及线面垂直的判定。
点评:空间中点线面的位置关系的运用,首先要熟练课本中线面的位置关系的判定和性质定理,面面的位置关系的判定和性质定理。然后进行逐一判定,属于基础题。

练习册系列答案
相关题目

