题目内容

如图，A是定圆x2+y2=1外的一个定点，点B在定圆上运动，求线段AB靠近A的三等分点M的轨迹．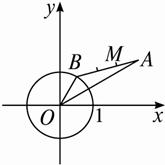

思路分析：由于点B在定圆x2+y2=1上运动，所以导致线段AB的运动，最终导致线段AB上的点M的运动，故点B可以看成是动点M(x，y)的相关动点，其相关规律是AM∶MB=1∶2，由此可用x、y及已知的A点坐标(设为(m，n))表示点B的坐标，然后将其代入已知圆的方程即可得M点的轨迹方程．

解：设M(x，y)、A(m，n)、B(a，b),

∵已知，∴有∴

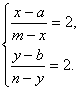∵B(a，b)是定圆x2+y2=1上的点,

∴a2+b2=1,即(3x-2m)2+(3y-2n)2=1．

    整理为（）2+（）2=.

∴点 M轨迹是一个以（）为圆心,为半径的圆.

方法归纳 所谓求轨迹方程，实质上是把曲线上动点的几何特征用动点坐标x，y的关系式表达出来，也就是完成“形”向“数”的转化，此例中，由于动点M(x，y)的特征不易直接由坐标表达式写出，需要借助与它密切相关的动点B的帮助，故称此解法为“相关点法”．

练习册系列答案
相关题目
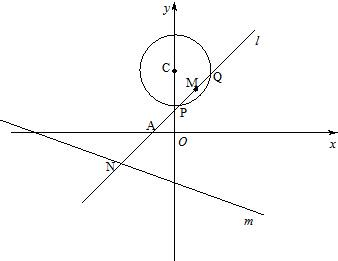精英家教网如图，已知定圆C：x2+（y-3）2=4，定直线m：x+3y+6=0，过A（-1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，M是PQ中点．
（Ⅰ）当l与m垂直时，求证：l过圆心C；
（Ⅱ）当|PQ|=2
3
时，求直线l的方程；
（Ⅲ）设t=
AM
•
AN
，试问t是否为定值，若为定值，请求出t的值；若不为定值，请说明理由．
如图，已知定圆C：x2+（y-3）2=4，定直线m：x+3y+6=0，过A（-1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，M是PQ中点．
（Ⅰ）当l与m垂直时，求证：l过圆心C；
（Ⅱ）当时，求直线l的方程；
（Ⅲ）设t=，试问t是否为定值，若为定值，请求出t的值；若不为定值，请说明理由．
如图，已知定圆C：x2+（y-3）2=4，定直线m：x+3y+6=0，过A（-1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，M是PQ中点．
（Ⅰ）当l与m垂直时，求证：l过圆心C；
（Ⅱ）当时，求直线l的方程；
（Ⅲ）设t=，试问t是否为定值，若为定值，请求出t的值；若不为定值，请说明理由．
如图，已知定圆C：x2+（y-3）2=4，定直线m：x+3y+6=0，过A（-1，0）的一条动直线l与直线相交于N，与圆C相交于P，Q两点，M是PQ中点．
（Ⅰ）当l与m垂直时，求证：l过圆心C；
（Ⅱ）当时，求直线l的方程；
（Ⅲ）设t=，试问t是否为定值，若为定值，请求出t的值；若不为定值，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网