题目内容
已知函数f(x)=|x|·(x+a)(a∈R)是奇函数。
(I)求a的值;
(II)设b>0,若函数f(x)在区间[-b,b]上最大值与最小值的差为b,求b的值。
(I)解:因为函数 的定义域为
的定义域为 ,且为奇函数,
,且为奇函数,
所以 ,
,
即 ,解得
,解得
验证可得 时,
时, 是奇函数。 (II)解:由(I),得
是奇函数。 (II)解:由(I),得
则当 时,
时, ,且
,且 在
在 上为增函数;
上为增函数;
当 时,
时, ,且
,且 在
在 上为增函数。
上为增函数。
所以当 时,
时, 取到最大值
取到最大值 ;当
;当 时,
时, 取到最小值
取到最小值 。
。
由题意,得 ,解得
,解得 或
或 (舍),
(舍),
故当 时,函数
时,函数 在区间
在区间 上最大值与最小值的差为
上最大值与最小值的差为 。
。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 不为1的等比数列
不为1的等比数列 满足
满足 ,则
,则 .
.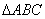 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 。
。 的值;
的值; ,
, 时,求
时,求 及
及 的长。
的长。 若f(x)=2,则x=_____________。
若f(x)=2,则x=_____________。 ,则在Sn中最大的负数为 ( )
,则在Sn中最大的负数为 ( ) 是等差数列,且
是等差数列,且 则k= .
则k= . 存入a元定期储蓄,若年利率为p且保持不变,并且每年到期的存款及利息均自动转为新一年定期,到2008年将所有的存款和利息全部取回,则可取回的钱的总数(元)为( ).
存入a元定期储蓄,若年利率为p且保持不变,并且每年到期的存款及利息均自动转为新一年定期,到2008年将所有的存款和利息全部取回,则可取回的钱的总数(元)为( ).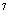 B a(1+p)
B a(1+p) C
C 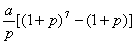 D
D 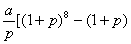 ]
] 吨,每次都购买
吨,每次都购买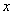 吨,运费为
吨,运费为 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为