Question

设f(n)＝1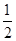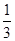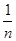＋＋＋ ＋ (n∈N^*)．

求证：f(1)＋f(2)＋ ＋f(n－1)＝n·[f(n)－1](n≥2，n∈N^*)．

 

Answer 1

【答案】

应用数学归纳法．

【解析】

试题分析：①当n＝2时，左边＝f(1)＝1，

右边＝2[1＋－1]＝1，

左边＝右边，等式成立．

②假设n＝k时，结论成立，即

f(1)＋f(2)＋ ＋f(k－1)＝k[f(k)－1]，

那么，当n＝k＋1时，

f(1)＋f(2)＋ ＋f(k－1)＋f(k)

＝k[f(k)－1]＋f(k)

＝(k＋1)f(k)－k

＝(k＋1)[f(k＋1)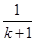－]－k

＝(k＋1)f(k＋1)－(k＋1)＝(k＋1)[f(k＋1)－1]，

所以当n＝k＋1时结论仍然成立．

所以f(1)＋f(2)＋ ＋f(n－1)＝n[f(n)－1](n≥2，n∈N^*)．

考点：本题主要考查数学归纳法。

点评：中档题，利用数学归纳法，注意遵循“两步一结”。对数学式子变形能力要求较高。