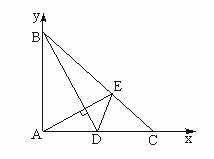
题目内容
等腰直角三角形ABC中,∠A=90°,BD是AC边上的中线,AE⊥BD交BC于E,用坐标法证明:∠ADB=
∠CDE.
证明:建立坐标系如图所示,设|AB|=|AC|=a,则在坐标系中各点坐标是A(0,0)、B(0,a)、C(a,0)、D(![]() ,0).
,0).
由斜率公式得kBD=![]() =-2.
=-2.
由已知AE⊥BD,得AE所在的直线方程是y=![]() x.
x.
E点的坐标(x0,y0)满足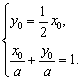 解得
解得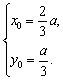
kDE=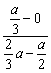 =
=![]() =2.
=2.
也就是tan∠CDE=2.
而tan∠ADB=tan(180°-∠CDB)=-tan∠CDB=-kBD=-(-2)=2,
∴tan∠CDE=tan∠ADB.
又∠CDE和∠ADB都是锐角,∴∠CDE=∠ADB.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
等腰直角三角形ABC,E、F分别是斜边BC的三等分点,则tan∠EAF=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 在等腰直角三角形ABC中,过直角顶点C在∠ACB内部任作一射线CM,与线段AB交于点M,求AM<AC的概率.
在等腰直角三角形ABC中,过直角顶点C在∠ACB内部任作一射线CM,与线段AB交于点M,求AM<AC的概率.