题目内容
（本小题满分12分）
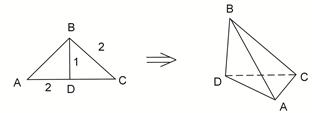
如图，平行四边形
中，
，
将
沿
折起到
的位置，使平面
平面
（I）求证：
；
（Ⅱ）求三棱锥
的侧面积.
（I）证明：
，平面
平面
平面
（Ⅱ）
解析试题分析：（I）证明：在
中，由
，所以
又平面平面
平面
平面
平面平面
平面
（Ⅱ）解：由（I）知
从而
在
中，
又
平面
平面
平面平面
，平面
而
平面
综上，三棱锥的侧面积，
考点：面面垂直的性质
点评：两面垂直，其中一个平面内垂直于交线的直线垂直于另外一面
练习册系列答案
阅读快车系列答案
相关题目
中，
为
边上的高，
，
，沿
翻折，使得
，得到几何体
。
；
与平面
所成角的正切值。
的长； （2）求cos<
>的值； （3）求证：A1B⊥C1M. 
，AB=BC=2AD=4，E、F分别是AB、CD上的点，且EF∥BC。设AE =
，G是BC的中点．沿EF将梯形ABCD翻折，使平面AEFD⊥平面EBCF （如图）．
，求
与
均为菱形， 
，且
，
平面
；
的余弦值。
平面
；
，AB=8，BC=6，点E是PC的中点，F在AD上且AF：FD=1：2．建立适当坐标系．
平面BCD；
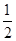AB，