题目内容
当x∈[0，π]时，y=sinx+cosx的单调递增区间是
- A.[0，
] - B.[0，
] - C.[
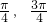] - D.[
]
A
分析：先根据两角和与差的正弦公式进行化简，再由正弦函数的单调性可得到-
≤x+≤，进而可求出x的范围，再结合题中所给x的范围确定答案．
解答：∵y=sinx+cosx=
sin（x+）
令-≤x+≤
∴-
，k∈Z
∵x∈[0，π]∴x∈[0，]
故选A．
点评：本题主要考查两角和与差的正弦公式和正弦函数的单调性的应用．考查基础知识的灵活应用．高考中三角函数的考查一般以基础为主，要强化基础的夯实．
分析：先根据两角和与差的正弦公式进行化简，再由正弦函数的单调性可得到-
≤x+≤，进而可求出x的范围，再结合题中所给x的范围确定答案．解答：∵y=sinx+cosx=
sin（x+）令-
≤x+≤∴-
，k∈Z∵x∈[0，π]∴x∈[0，
]故选A．
点评：本题主要考查两角和与差的正弦公式和正弦函数的单调性的应用．考查基础知识的灵活应用．高考中三角函数的考查一般以基础为主，要强化基础的夯实．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜定义域R的函数f（x）满足f（x+2）=3f（x），当x∈[0，2]时，f（x）=x2-2x，若x∈[-4，-2]时，f(x)≥
(
-t)恒成立，则实数t的取值范围是（ ）
| 1 |
| 18 |
| 3 |
| t |
| A、（-∞，-1]∪（0，3] | ||||
B、(-∞，-
| ||||
| C、[-1，0）∪[3，+∞） | ||||
D、[-
|