题目内容
已知数列的通项公式an=4n+7,则其中三位数的个数有________________个.
解析:由题意知100≤an≤999,
即100≤4n+7≤999,解得23
≤n≤248.
又n∈N*,∴n=24,25,…,248,共225个.
答案:225
练习册系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
已知数列的通项公式an=
(n∈N*)，则数列{an}的前30项中最大值和最小值分别是（ ）
n-
| ||
n-
|
| A、a10，a9 |
| B、a10，a30 |
| C、a1，a30 |
| D、a1，a9 |
已知数列
的通项公式
,设其前n项和为
，则使
成立的自然
数
有 （ ）
| A．最大值15 | B．最小值15 | C．最大值16 | D．最小值16 |
的通项公式为
，设其前
项和为
，则使
成立的最小自然数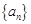
的通项公式为
，则数列
成等比数列是数列
的通项公式为
的( ▲ )