题目内容
已知函数f(x)=4cosωx·sin(ωx+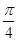 )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.
(1)求ω的值;
(2)讨论f(x)在区间[0,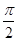 ]上的单调性.
]上的单调性.
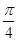 )(ω>0)的最小正周期为π.
)(ω>0)的最小正周期为π.(1)求ω的值;
(2)讨论f(x)在区间[0,
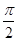 ]上的单调性.
]上的单调性.(1)ω=1
(2)f(x)在区间[0,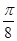 ]上单调递增,在区间[
]上单调递增,在区间[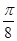 ,
,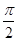 ]上单调递减.
]上单调递减.
(2)f(x)在区间[0,
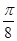 ]上单调递增,在区间[
]上单调递增,在区间[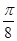 ,
,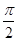 ]上单调递减.
]上单调递减.解:(1)f(x)=4cosωx·sin(ωx+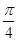 )
)
=2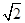 sinωx·cosωx+2
sinωx·cosωx+2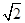 cos2ωx
cos2ωx
=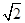 (sin2ωx+cos2ωx)+
(sin2ωx+cos2ωx)+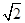
=2sin(2ωx+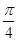 )+
)+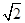 .
.
∵f(x)的最小正周期为π,且ω>0,
从而有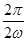 =π,故ω=1.
=π,故ω=1.
(2)由(1)知f(x)=2sin(2x+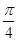 )+
)+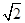 .
.
若0≤x≤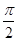 ,则
,则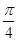 ≤2x+
≤2x+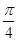 ≤
≤ .
.
当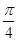 ≤2x+
≤2x+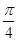 ≤
≤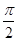 ,即0≤x≤
,即0≤x≤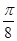 时,f(x)单调递增;
时,f(x)单调递增;
当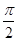 ≤2x+
≤2x+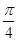 ≤
≤ ,即
,即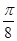 ≤x≤
≤x≤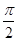 时,f(x)单调递减.
时,f(x)单调递减.
综上可知,f(x)在区间[0,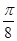 ]上单调递增,在区间[
]上单调递增,在区间[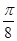 ,
,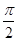 ]上单调递减.
]上单调递减.
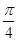 )
)=2
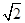 sinωx·cosωx+2
sinωx·cosωx+2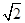 cos2ωx
cos2ωx=
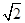 (sin2ωx+cos2ωx)+
(sin2ωx+cos2ωx)+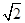
=2sin(2ωx+
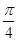 )+
)+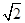 .
.∵f(x)的最小正周期为π,且ω>0,
从而有
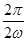 =π,故ω=1.
=π,故ω=1.(2)由(1)知f(x)=2sin(2x+
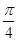 )+
)+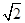 .
.若0≤x≤
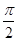 ,则
,则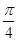 ≤2x+
≤2x+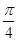 ≤
≤ .
.当
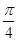 ≤2x+
≤2x+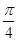 ≤
≤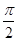 ,即0≤x≤
,即0≤x≤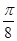 时,f(x)单调递增;
时,f(x)单调递增;当
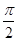 ≤2x+
≤2x+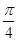 ≤
≤ ,即
,即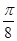 ≤x≤
≤x≤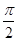 时,f(x)单调递减.
时,f(x)单调递减.综上可知,f(x)在区间[0,
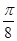 ]上单调递增,在区间[
]上单调递增,在区间[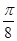 ,
,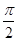 ]上单调递减.
]上单调递减.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 .
. 的最小正周期;
的最小正周期; 时,求
时,求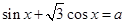 在闭区间[0,2
在闭区间[0,2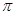 ]上恰有三个解
]上恰有三个解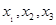 ,则
,则 .
.  的最小值是( )
的最小值是( )




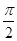 )与g(x)=cos(ωx-
)与g(x)=cos(ωx-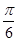 )(ω>0)的图象具有相同的对称中心,则φ=( )
)(ω>0)的图象具有相同的对称中心,则φ=( )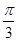
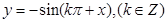 是奇函数;
是奇函数;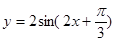 的图象关于点
的图象关于点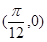 对称;
对称;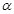 、
、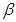 是第一象限的角,且
是第一象限的角,且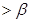 ,则
,则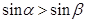 .
.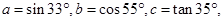 则
则



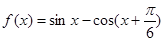 的值域为
的值域为