题目内容
6.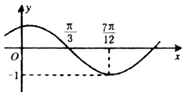 若f(x)=Asin(ωx+ϕ)(其中A>0,|φ|$<\frac{π}{2}$)的图象如图,为了得到$g(x)=sin(2x-\frac{π}{3})$的图象,则需将f(x)的图象( )
若f(x)=Asin(ωx+ϕ)(其中A>0,|φ|$<\frac{π}{2}$)的图象如图,为了得到$g(x)=sin(2x-\frac{π}{3})$的图象,则需将f(x)的图象( )| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
分析 由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式,再利用y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:根据f(x)=Asin(ωx+ϕ)(其中A>0,|φ|$<\frac{π}{2}$)的图象,可得A=1,
$\frac{1}{4}•\frac{2π}{ω}$=$\frac{7π}{12}$-$\frac{π}{3}$,∴ω=2.
再根据五点法作图可得2•$\frac{π}{3}$+φ=π,∴φ=$\frac{π}{3}$,∴f(x)=sin(2x+$\frac{π}{3}$).
故把f(x)=sin(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{3}$个单位,可得y=sin[2(x-$\frac{π}{3}$)+$\frac{π}{3}$]=sin(2x-$\frac{π}{3}$)=g(x)的图象,
故选:B.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
11.在空间直角坐标系中,点P(3,2,5)关于yOz平面对称的点的坐标为( )
| A. | (-3,2,5) | B. | (-3,-2,5) | C. | (3,-2,-5) | D. | (-3,2,-5) |
15.函数$f(x)=\frac{{\sqrt{3}+tanx}}{{1-\sqrt{3}tanx}}$( )
| A. | 定义域是$\{x|x≠kπ+\frac{π}{6},(k∈Z)\}$ | B. | 值域是R | ||
| C. | 在其定义域上是增函数 | D. | 最小正周期是π |
16.已知随机变量服从正态分布N(0,σ2),且P(-2≤ξ≤0)=0.4,则P(ξ>2)=( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.6 |