题目内容
以椭圆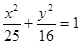 的焦点为顶点,离心率为
的焦点为顶点,离心率为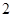 的双曲线方程( )
的双曲线方程( )
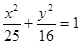 的焦点为顶点,离心率为
的焦点为顶点,离心率为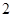 的双曲线方程( )
的双曲线方程( )A.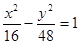 | B. |
C.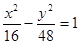 或 或 | D.以上都不对 |
B
知识点:椭圆焦点,双曲线方程的求法,离心率
解:椭圆
 的焦点为(3,0)和(-3,0)由题意知道双曲线的顶点坐标为(3,0)
的焦点为(3,0)和(-3,0)由题意知道双曲线的顶点坐标为(3,0)(-3,0)所以a=3.由双曲线的离心率e=2,得
 ,解得c=6,
,解得c=6,
 双曲线方程为
双曲线方程为 ,选B.
,选B.点评:此题要熟练掌握椭圆,双曲线的顶点,焦点的计算。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
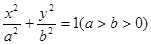 的右焦点F为圆心,
的右焦点F为圆心,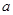 为半径的圆与直线
为半径的圆与直线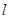 :
: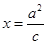 (其中
(其中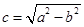 )交于不同的两点,则该椭圆的离心率的取值范围是( )
)交于不同的两点,则该椭圆的离心率的取值范围是( )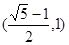
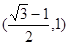
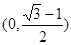
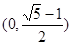
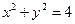 ,求斜率等于1的圆的切线的方程;(6分)
,求斜率等于1的圆的切线的方程;(6分)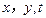 ,满足
,满足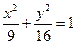 且
且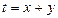 ,求
,求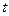 的取值范围;(6分)
的取值范围;(6分)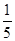

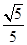
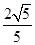
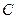 的中心为坐标原点
的中心为坐标原点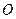 ,焦点在
,焦点在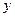 轴上,焦点到相应准线的距离以及离心率均为
轴上,焦点到相应准线的距离以及离心率均为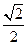 ,直线
,直线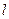 与
与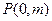 ,与椭圆
,与椭圆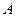 、
、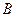 ,且
,且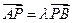 .
.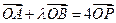 ,求
,求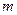 的取值范围.
的取值范围.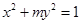 的离心率为
的离心率为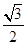 ,则它的长半轴长为( )
,则它的长半轴长为( )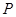 在椭圆
在椭圆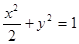 上,
上,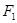 、
、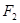 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且 ,则
,则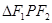 的面积是( )
的面积是( )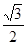
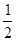
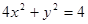 的准线方程是( )
的准线方程是( )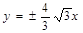

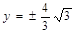
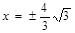
 的离心率为
的离心率为


