题目内容
已知椭圆 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点, 的重心为G,内心I,且有
的重心为G,内心I,且有 (其中
(其中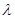 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )
A. | B. | C.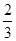 | D. |
A
解析试题分析:设P( ),∵G为
),∵G为 的重心,∴G点坐标为 G(
的重心,∴G点坐标为 G( ),∵
),∵ ,∴IG∥x轴,∴I的纵坐标为
,∴IG∥x轴,∴I的纵坐标为 ,在焦点
,在焦点 中,
中, ,
, =2c,∴
=2c,∴ =
= •
• •
• ,又∵I为
,又∵I为 的内心,∴I的纵坐标
的内心,∴I的纵坐标 即为内切圆半径,内心I把
即为内切圆半径,内心I把 分为三个底分别为
分为三个底分别为 的三边,高为内切圆半径的小三角形,∴
的三边,高为内切圆半径的小三角形,∴ =
= (
( )
) ,∴
,∴ •
• •
• =
= (
( )
) 即
即 •2c•
•2c• =
= (
( )
) ,∴2c=a,∴椭圆C的离心率e=
,∴2c=a,∴椭圆C的离心率e= ,故选A
,故选A
考点:本题考查了离心率的求法
点评:求解椭圆中的离心率时往往用到椭圆的概念,此类问题还用到重心坐标公式,三角形内心的意义及其应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若双曲线 的离心率为2,则双曲线
的离心率为2,则双曲线 的离心率为( )
的离心率为( )
A. | B. | C.2 | D. |
抛物线 的焦点F是椭圆
的焦点F是椭圆 的一个焦点,且它们的交点M到F的距离为
的一个焦点,且它们的交点M到F的距离为 ,则椭圆的离心率为
,则椭圆的离心率为
A. | B. | C. | D. |
已知
 的顶点
的顶点 、
、 分别为双曲线
分别为双曲线 的左右焦点,顶点
的左右焦点,顶点 在双曲线
在双曲线 上,则
上,则 的值等于
的值等于
A. | B. | C. | D. |
若双曲线 的左焦点在抛物线y2=2px的准线上,则p的值为( )
的左焦点在抛物线y2=2px的准线上,则p的值为( )
| A.2 | B.3 | C.4 | D.6 |
 的左右焦点分别为
的左右焦点分别为 ,若椭圆
,若椭圆 上恰好有6个不同的点
上恰好有6个不同的点 ,使得
,使得 为等腰三角形,则椭圆
为等腰三角形,则椭圆



 的焦点相同,则双曲线C的标准方程是( )
的焦点相同,则双曲线C的标准方程是( )



 ,它的一个焦点为F1,则满足
,它的一个焦点为F1,则满足 为等边三角形的椭圆的离心率是( )
为等边三角形的椭圆的离心率是( )



 、
、 与双曲线
与双曲线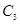 、
、 的离心率分别是
的离心率分别是 、
、 与
与 、
、 , 则
, 则



