题目内容
若两个非零向量 ,
, 满足|
满足| +
+ |=|
|=| -
- |=2|
|=2| |,则向量
|,则向量 +
+ 与
与 -
- 的夹角为
的夹角为
- A.30°
- B.60°
- C.90°
- D.120°
D
分析:设向量 +
+ 与
与 -
- 的夹角为θ,由|
的夹角为θ,由| +
+ |=|
|=| -
- |=2|
|=2| |,可得
|,可得 ,
, ,代入向量的夹角公式cosθ=
,代入向量的夹角公式cosθ= 可求
可求
解答:设向量 +
+ 与
与 -
- 的夹角为θ
的夹角为θ
∵| +
+ |=|
|=| -
- |=2|
|=2| |,
|,
∴ =
= =
=
∴ ,
,
∴( )•(
)•( )=
)= =-2
=-2
∴cosθ= =
= =
=
∵0≤θ≤π
∴θ=120°
故选D
点评:本题主要考查了向量的数量积的性质的综合应用,向量夹角公式的应用,属于中档试题
分析:设向量
 +
+ 与
与 -
- 的夹角为θ,由|
的夹角为θ,由| +
+ |=|
|=| -
- |=2|
|=2| |,可得
|,可得 ,
, ,代入向量的夹角公式cosθ=
,代入向量的夹角公式cosθ= 可求
可求解答:设向量
 +
+ 与
与 -
- 的夹角为θ
的夹角为θ∵|
 +
+ |=|
|=| -
- |=2|
|=2| |,
|,∴
 =
= =
=
∴
 ,
,
∴(
 )•(
)•( )=
)= =-2
=-2
∴cosθ=
 =
= =
=
∵0≤θ≤π
∴θ=120°
故选D
点评:本题主要考查了向量的数量积的性质的综合应用,向量夹角公式的应用,属于中档试题

练习册系列答案
相关题目
 ,
, 满足
满足 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( ) B.
B. C.
C. D.
D.
 ,
, 满足|
满足| ,则
,则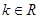 ,且
,且 ,则
,则
 ,则
,则 或
或
 ,满足|
,满足| |
| |
| |,则
|,则
 |
|