题目内容
已知双曲线C:(Ⅰ)求双曲线C的方程;
(Ⅱ)若双曲线C上的点P满足![]() =1,求
=1,求![]() 的值;
的值;
(Ⅲ)若直线y=kx+m(k≠0,m≠0)与双曲线C交于不同两点M、N,且线段MN的垂直平分线过点A(0,-1),求实数m的取值范围.
本小题考查双曲线方程,直线与圆锥曲线关系及向量的应用.
解:(Ⅰ)由 ||EF1|-|EF2||=2![]() a=
a=![]() .
.
∵c-a=2-![]() ,∴c=2.∴b2=c2-a2=1.
,∴c=2.∴b2=c2-a2=1.
∴双曲线C的方程为![]() =1.
=1.
(Ⅱ)设|![]() |=r1,|
|=r1,|![]() |=r2,不妨设r1>r2>0,∠F1PF2=θ.
|=r2,不妨设r1>r2>0,∠F1PF2=θ.
由![]() ·
·![]() =1
=1![]() r1r2cosθ=1.
r1r2cosθ=1.
又r1-r2=2![]()
![]()
![]() -2r1r2=12.
-2r1r2=12.
在△PF1F2中,由余弦定理得16=![]() -2r1r2cosθ.
-2r1r2cosθ.
∴r1r2=3. ∴|![]() |·|
|·|![]() |=3.
|=3.
(Ⅲ)联立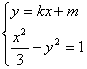 ,整理得
,整理得
(1-3k2)x2-6kmx-3m2-3=0.
∵直线与双曲线有两个不同交点,
∴1-3k2≠0且△=12(m2+1-3k2)>0. ①
设M(x1,y1),N(x2,y2),MN的中点为B (x0,y0),则x1+x2=![]() ,
,
∴x0=![]() ,∴y0=k x0+m=
,∴y0=k x0+m=![]() .
.
由题意AB⊥MN,∴kAB=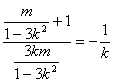 (k≠0,m≠0).
(k≠0,m≠0).
整理得3k2+4m+1. ②
将②式代入①式,得m2-4m>0,∴m>4或m<0.
又3k2=4m+1>0(k≠0)即m>![]() .
.
∴m的取值范围为m,4或![]() <m<0.
<m<0.

练习册系列答案
相关题目
 =1(a>0,b>0)的离心率为
=1(a>0,b>0)的离心率为 ,右准线方程为x=
,右准线方程为x=
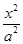 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
)
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为(
) -
-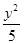 =1
B.
=1
B.  -
- =1 C.
=1 C.  -
- =1
=1 -
- =1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为
=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C的方程为 -
- =1 B、
=1 B、 -
- =1
C、
=1
C、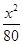 -
- =1[w~#
=1[w~#