题目内容
已知![]() .
.
(1)若![]() ,求方程
,求方程![]() 的解;
的解;
(2)若关于![]() 的方程
的方程![]() 在(0,2)上有两个解
在(0,2)上有两个解![]() ,求
,求![]() 的取值范围,并证明
的取值范围,并证明![]() .
.
解:(1)![]() ,
,![]() =0有实根,则
=0有实根,则![]() 即
即![]()
故![]()
令![]() 解得
解得![]() 或
或![]()
(2)当![]() ,
,![]() 有两解,又
有两解,又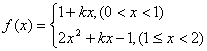 ,因
,因![]() 有两种情况:①可以在(0,1)上有一解,在
有两种情况:①可以在(0,1)上有一解,在![]() 有一解;②或者在
有一解;②或者在![]() 上有两解。
上有两解。
①显然当x=1时,不满足题意,当一解在(0,1)另一解在![]() 时需满足
时需满足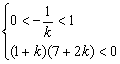 ;解得
;解得![]()
(2)当两解均在![]() 时,对于
时,对于![]() ,得
,得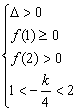 解得
解得![]()
综上:![]()
证明:解得![]() ,
,
故![]() =
=![]() ,
,
即证![]() ,,即证
,,即证![]()
又![]() ,∴原不等式成立,即有
,∴原不等式成立,即有![]() .
.

练习册系列答案
相关题目

 ,求
,求 实数的值;
实数的值; ,求实数
,求实数
 ,求函数
,求函数 在点(0,
在点(0, )处的切线方程;
)处的切线方程; ,使得
,使得 的极大值为3.若存在,求出
的极大值为3.若存在,求出 ,
, ,求
,求 的值;
的值; ,求
,求 中含
中含 项的系数
项的系数
 ,求m的值;
,求m的值; ,求m的取值范围。
,求m的取值范围。