题目内容
 已知F1、F2分别是椭圆
已知F1、F2分别是椭圆 (a>b>0)的左、右焦点,M、N分别是直线
(a>b>0)的左、右焦点,M、N分别是直线 (m是大于零的常数)与x轴、y轴的交点,线段MN的中点P在椭圆C上.
(m是大于零的常数)与x轴、y轴的交点,线段MN的中点P在椭圆C上.
(Ⅰ)求常数m的值;
(Ⅱ)试探究直线l与椭圆C是否还存在异于点P的其它公共点?请说明理由;
(Ⅲ)当a=2时,试求△PF1F2面积的最大值,并求△PF1F2面积取得最大值时椭圆C的方程.
 解:(Ⅰ)由已知可得M(ma,0)、N(0,mb),
解:(Ⅰ)由已知可得M(ma,0)、N(0,mb),
故MN的中点为 ,
,
又点P在椭圆C上,∴ ,所以
,所以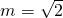
(Ⅱ)(解法一)由(Ⅰ)得 ,
,
与方程C联立得: ,
,
即 ,
,
由于 ,
,
∴此方程有两个相等实根 ,
,
故直线l与椭圆C相切,切点为 ,
,
除此之外,不存在其他公共点
(解法二)由(Ⅰ)得 ,与方程C联立得:
,与方程C联立得:
所以 ,则
,则
∴ 和
和 是方程
是方程 的两根,
的两根,
又 ,∴此方程有两个相等实根,即
,∴此方程有两个相等实根,即 ,
,
∴直线l与椭圆C的公共点是唯一的点 ,
,
即除点P以外,不存在其他公共点
(Ⅲ)当a=2时, =
= ,
,
所以
 ,
,
当且仅当 时,等式成立,故
时,等式成立,故
此时,椭圆C的方程为:
分析:(Ⅰ)由已知可得M(ma,0)、N(0,mb),从而可得MN的中点为P的坐标,利用点P在椭圆C上,即可求常数m的值;
(Ⅱ)(解法一)由(Ⅰ)得
 ,与方程C联立消元,由此可得直线l与椭圆C相切时切点的坐标;
,与方程C联立消元,由此可得直线l与椭圆C相切时切点的坐标;(解法二)由(Ⅰ)得
 ,与方程C联立,可得
,与方程C联立,可得 ,从而
,从而 和
和 是方程
是方程 的两根,由此可得直线l与椭圆C的公共点是唯一的点P;
的两根,由此可得直线l与椭圆C的公共点是唯一的点P;(Ⅲ)当a=2时,表示△PF1F2面积,利用基本不等式,可求△PF1F2面积的最大值,从而可得椭圆C的方程.
点评:本题考查直线与椭圆的位置关系,考查三角形面积的计算,考查基本不等式的运用,联立直线与椭圆方程是关键.

练习册系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: