题目内容
已知A、B是椭圆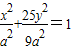 上的两点,F2是椭圆的右焦点,如果|AF2|+|BF2|=
上的两点,F2是椭圆的右焦点,如果|AF2|+|BF2|=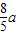 ,AB的中点到椭圆左准线距离为
,AB的中点到椭圆左准线距离为 ,则椭圆的方程 .
,则椭圆的方程 .
【答案】分析:由椭圆的第一定义求出|AF1|+|BF1|,利用椭圆的第二定义及梯形中位线的性质求出a的值,从而得到椭圆方程.
解答:解:∵|AF2|+|BF2|= ,∴2a-|AF1|+2a-|BF1|=
,∴2a-|AF1|+2a-|BF1|= ,∴|AF1|+|BF1|=
,∴|AF1|+|BF1|= a,
a,
记AB的中点为M,A、B、M在椭圆左准线上的射影分别为A1、B1,M1,
由椭圆第二定义知:|AF1|=e|AA1|,|BF1|=e|BB1|,于是有:e(|AA1|+|BB1|)= ,而e=
,而e= ,
,
∴|AA1|+|BB1|=3a∴2|MM1|=3a,又|MM1|= ,∴a=1,故椭圆方程为 x2+
,∴a=1,故椭圆方程为 x2+ .
.
故答案为 x2+ .
.
点评:本题考查椭圆的第一定义、第二定义,椭圆的标准方程,以及梯形的中位线的性质.
解答:解:∵|AF2|+|BF2|=
 ,∴2a-|AF1|+2a-|BF1|=
,∴2a-|AF1|+2a-|BF1|= ,∴|AF1|+|BF1|=
,∴|AF1|+|BF1|= a,
a,记AB的中点为M,A、B、M在椭圆左准线上的射影分别为A1、B1,M1,
由椭圆第二定义知:|AF1|=e|AA1|,|BF1|=e|BB1|,于是有:e(|AA1|+|BB1|)=
 ,而e=
,而e= ,
,∴|AA1|+|BB1|=3a∴2|MM1|=3a,又|MM1|=
 ,∴a=1,故椭圆方程为 x2+
,∴a=1,故椭圆方程为 x2+ .
.故答案为 x2+
 .
.点评:本题考查椭圆的第一定义、第二定义,椭圆的标准方程,以及梯形的中位线的性质.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
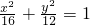 上的两点,F2是其右焦点,如果|AF2|+|BF2|=8,则AB的中点到椭圆左准线的距离为
上的两点,F2是其右焦点,如果|AF2|+|BF2|=8,则AB的中点到椭圆左准线的距离为 上的两点,F2是椭圆的右焦点,如果|AF2|+|BF2|=
上的两点,F2是椭圆的右焦点,如果|AF2|+|BF2|= ,AB的中点到椭圆左准线距离为
,AB的中点到椭圆左准线距离为 ,则椭圆的方程 ________.
,则椭圆的方程 ________. 上的两点,F2是其右焦点,如果|AF2|+|BF2|=8,则AB的中点到椭圆左准线的距离为( )
上的两点,F2是其右焦点,如果|AF2|+|BF2|=8,则AB的中点到椭圆左准线的距离为( ) 上的两点,F2是椭圆的右焦点,如果|AF2|+|BF2|=
上的两点,F2是椭圆的右焦点,如果|AF2|+|BF2|= ,AB的中点到椭圆左准线距离为
,AB的中点到椭圆左准线距离为 ,则椭圆的方程 .
,则椭圆的方程 .