题目内容
已知函数 .
.
(1)若f(x)=2,求x的值;
(2)若3tf(2t)+mf(t)≥0对于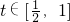 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
解(1)当x<0时,f(x)=3x-3x=0,
∴f(x)=2无解;
当x>0时, ,
, ,
,
∴(3x)2-2•3x-1=0,
∴ .
.
∵3x>0,
∴ (舍).
(舍).
∴ ,
,
∴ .
.
(2)∵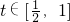 ,
,
∴ ,
,
∴ .
.
∴ ,
,
即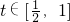 时m>-32t-1恒成立
时m>-32t-1恒成立
又-32t-1∈[-10,-4],
∴m>-4.
∴实数m的取值范围为(-4,+∞).
分析:(1)当x≤0时得到f(x)=0而f(x)=2,所以无解;当x>0时解出f(x)=2求出x即可;
(2)由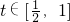 时,3tf(2t)+mf(t)≥0恒成立得到,得到f(t)=
时,3tf(2t)+mf(t)≥0恒成立得到,得到f(t)= ,代入得到m的范围即可.
,代入得到m的范围即可.
点评:考查学生理解函数恒成立的条件,以及会根据条件求函数值的能力.
∴f(x)=2无解;
当x>0时,
 ,
, ,
,∴(3x)2-2•3x-1=0,
∴
 .
.∵3x>0,
∴
 (舍).
(舍).∴
 ,
,∴
 .
.(2)∵
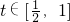 ,
,∴
 ,
,∴
 .
.∴
 ,
,即
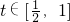 时m>-32t-1恒成立
时m>-32t-1恒成立又-32t-1∈[-10,-4],
∴m>-4.
∴实数m的取值范围为(-4,+∞).
分析:(1)当x≤0时得到f(x)=0而f(x)=2,所以无解;当x>0时解出f(x)=2求出x即可;
(2)由
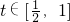 时,3tf(2t)+mf(t)≥0恒成立得到,得到f(t)=
时,3tf(2t)+mf(t)≥0恒成立得到,得到f(t)= ,代入得到m的范围即可.
,代入得到m的范围即可.点评:考查学生理解函数恒成立的条件,以及会根据条件求函数值的能力.

练习册系列答案
相关题目
 .
. .
. .
. .
. .
. .
. .
.