题目内容
已知四面体 的所有棱长都相等,它的俯视图如下图所示,是一个边长为
的所有棱长都相等,它的俯视图如下图所示,是一个边长为 的正方形;则四面体
的正方形;则四面体 外接球的表面积为( )
外接球的表面积为( )
A. | B. | C. | D.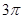 |
A
解析试题分析:根据题意,根据题意,画出图形,
结合题目所给数据,求出正视图的三边的长,可求其面积.
解:这个正四面体的位置是AC放在桌面上, BD平行桌面,它的正视图是和几何体如图,则正视图 BD= ,DO=BO=
,DO=BO= ∴其外接球的半径为
∴其外接球的半径为 故其球的表面积公式为,故答案为
故其球的表面积公式为,故答案为 ,选A.
,选A.
考点:球的表面积和三视图
点评:主要是考查了三视图的运用,以及球的表面积公式的运用,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知某个几何体的三视图如右图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( ).
A. cm3 cm3 | B. cm3 cm3 |
| C.2 000 cm3 | D.4 000 cm3 |
如图⑴、⑵、⑶、⑷为四个几何体的三视图,根据三视图可以判断这四个几何体依次分别为
| A.三棱台、三棱柱、圆锥、圆台 | B.三棱台、三棱锥、圆锥、圆台 |
| C.三棱柱、正四棱锥、圆锥、圆台 | D.三棱柱、三棱台、圆锥、圆台 |
棱长都是1的三棱锥的表面积为( )
A. | B.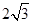 | C.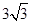 | D. |
一个几何体的三视图如右图所示,则该几何体的体积为( )
| A.16 | B.12 | C.8 | D.4 |
如图是水平放置的平面图形的斜二测直观图,其原来平面图形面积是( )
A.2 | B.4 | C.4 | D.8 |
某几何体的三视图如下,则几何体的表面积为( )
A.28+6 | B.30+6 | C.56+12 | D.60+12 |
一个空间几何体的三视图如图所示,则该几何体的表面积为( )
| A.48 | B.32+8 | C.48+8 | D.80 |



