题目内容
若a是1+2b与1-2b的等比中项,则
的最大值为( )
| 2ab |
| |a|+2|b| |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由a是1+2b与1-2b的等比中项得到4|ab|≤1,再由基本不等式法求得.
解答:解:a是1+2b与1-2b的等比中项,则a2=1-4b2?a2+4b2=1≥4|ab|.
∴|ab|≤
.
∵a2+4b2=(|a|+2|b|)2-4|ab|=1.
∴
=
≤
=
=
=
∵|ab|≤
∴
≥4,
∴
=
.
故选B.
∴|ab|≤
| 1 |
| 4 |
∵a2+4b2=(|a|+2|b|)2-4|ab|=1.
∴
| 2ab |
| |a|+2|b| |
| 2ab | ||
|
| 2|ab| | ||
|
|
|
|
∵|ab|≤
| 1 |
| 4 |
∴
| 1 |
| |ab| |
∴
| 2ab |
| |a|+2|b| |
| ||
. |
|
| ||
| 4 |
故选B.
点评:本题考查等比中项以及不等式法求最值问题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
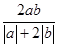 的最大值为( )
的最大值为( ) B、
B、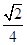 C、
C、 D、
D、
 的最大值为( )
的最大值为( ) B.
B. C.
C. D.
D.