题目内容
(本小题满分12分)
已知定义域为 的函数
的函数 是奇函数.
是奇函数.
(1)求 的值;
的值;
(2)若对任意的 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1) (2)
(2)
解析试题分析:解:(1)因为 是定义在
是定义在 上的奇函数,所以
上的奇函数,所以
即: 解得:
解得: …………2分
…………2分
所以
因为
所以 是奇函数,故
是奇函数,故 …………4分
…………4分
(2)由(1)得 ,易知
,易知 是减函数.
是减函数.
原不等式可以化为: …………8分
…………8分
因为 是定义在
是定义在 上的减函数.
上的减函数.
所以 ,即
,即 对
对 恒成立.
恒成立.
因为 …………10分
…………10分
所以 …………12分
…………12分
考点:本试题考查了函数的奇偶性和单调性。
点评:解决该试题的关键是利用函数的单调性来分析求解抽象不等式,来得到不等式的解集,同时利用分离参数是思想来得到参数的取值范围,属于中档题。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
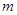 是实数,
是实数,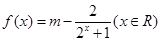 ,
, 为奇函数,求
为奇函数,求 上为单调递增函数;
上为单调递增函数;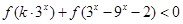 对任意
对任意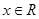 恒成立,求实数
恒成立,求实数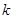 的取值范围。
的取值范围。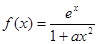 ,其中
,其中 为正实数。
为正实数。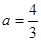 时,求
时,求 的极值点;
的极值点;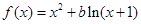 .
. ,都有
,都有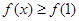 成立,求实数
成立,求实数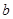 的值;
的值; 在定义域上是单调函数,求
在定义域上是单调函数,求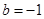 ,证明对任意正整数
,证明对任意正整数 ,不等式
,不等式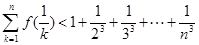 都成立.
都成立. (
(
 R).
R). ,求函数
,求函数 的极值;
的极值; 上有两个零点,若存在,求出
上有两个零点,若存在,求出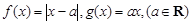 .
. 的奇偶性;(4分)
的奇偶性;(4分) 的方程
的方程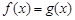 有两解,求实数
有两解,求实数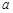 的取值范围;(6分)
的取值范围;(6分)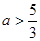 ,记
,记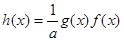 ,试求函数
,试求函数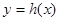 在区间
在区间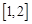 上的最大值.(10分)
上的最大值.(10分) 。
。 对任意的实数
对任意的实数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,且
,且 在
在 上单调递增,求实数
上单调递增,求实数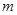 的取值范围。
的取值范围。 ,函数
,函数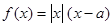 .
. 在
在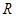 上的奇偶性;
上的奇偶性; 上的最大值。
上的最大值。
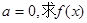 的单调区间;
的单调区间; 存在极值,且所有极值之和大于
存在极值,且所有极值之和大于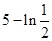 ,求a的取值范围。
,求a的取值范围。