题目内容
 如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上(含原点)上滑动,则
如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上(含原点)上滑动,则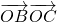 的最大值是
的最大值是
- A.1
- B.

- C.2
- D.

C
分析:令∠OAD=θ,由边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上,可得出B,C的坐标,由此可以表示出两个向量,算出它们的内积即可.
解答:如图令∠OAD=θ,由于AD=1故0A=cosθ,OD=sinθ,
如图∠BAX= -θ,AB=1,故xB=cosθ+cos(
-θ,AB=1,故xB=cosθ+cos( -θ)=cosθ+sinθ,yB=sin(
-θ)=cosθ+sinθ,yB=sin( -θ)=cosθ,
-θ)=cosθ,
故 =(cosθ+sinθ,cosθ)
=(cosθ+sinθ,cosθ)
同理可求得C(sinθ,cosθ+sinθ),即 =(sinθ,cosθ+sinθ),
=(sinθ,cosθ+sinθ),
∴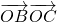 =(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=1+sin2θ,故
=(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=1+sin2θ,故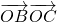 的最大值是2,
的最大值是2,
故答案是 2.
点评:本题主要考查向量在几何中的应用,设角引入坐标是解题的关键,由于向量的运算与坐标关系密切,所以在研究此类题时应该想到设角来表示点的坐标,属于中档题.
分析:令∠OAD=θ,由边长为1的正方形ABCD的顶点A、D分别在x轴、y轴正半轴上,可得出B,C的坐标,由此可以表示出两个向量,算出它们的内积即可.
解答:如图令∠OAD=θ,由于AD=1故0A=cosθ,OD=sinθ,
如图∠BAX=
 -θ,AB=1,故xB=cosθ+cos(
-θ,AB=1,故xB=cosθ+cos( -θ)=cosθ+sinθ,yB=sin(
-θ)=cosθ+sinθ,yB=sin( -θ)=cosθ,
-θ)=cosθ,故
 =(cosθ+sinθ,cosθ)
=(cosθ+sinθ,cosθ)同理可求得C(sinθ,cosθ+sinθ),即
 =(sinθ,cosθ+sinθ),
=(sinθ,cosθ+sinθ),∴
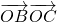 =(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=1+sin2θ,故
=(cosθ+sinθ,cosθ)•(sinθ,cosθ+sinθ)=1+sin2θ,故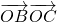 的最大值是2,
的最大值是2,故答案是 2.
点评:本题主要考查向量在几何中的应用,设角引入坐标是解题的关键,由于向量的运算与坐标关系密切,所以在研究此类题时应该想到设角来表示点的坐标,属于中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST=
如图放置的边长为1的正方形PABC沿x轴滚动.设顶点p(x,y)的轨迹方程是y=f(x),设f(x)的最小正周期为T,y=f(x)在其两个相邻零点间的图象与x轴所围区域的面积为S,则ST= 如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴(含坐标原点上滑动,则
如图放置的边长为1的正方形ABCD的顶点A、D分别在x轴、y轴(含坐标原点上滑动,则

