题目内容
已知函数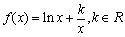
(1)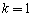 时函数
时函数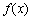 的单调性;
的单调性;
(2)若 恒成立,求实数
恒成立,求实数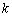 的取值范围;
的取值范围;
(3)设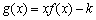 ,若对任意的两个实数
,若对任意的两个实数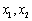 满足
满足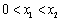 ,总存在
,总存在 ,使得
,使得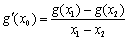 成立,证明:
成立,证明: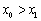
解析:
(1)当 时,函数
时,函数 ,
,
则
 .
.
当 时,
时, ,当
,当 时,
时, 1,
1,
则函数 的单调递减区间为(0,1),单调递增区间为(1,
的单调递减区间为(0,1),单调递增区间为(1, .
.
(2) 恒成立,即
恒成立,即 恒成立,整理得
恒成立,整理得 恒成立.
恒成立.
设 ,则
,则 ,令
,令 ,得
,得 .当
.当 时,
时, ,函数
,函数 单调递增,当
单调递增,当
 时,
时, ,函数
,函数 单调递减,因此当
单调递减,因此当 时,
时, 取得最大值1,因而
取得最大值1,因而 .
.
(3) ,
, .
.
因为对任意的 总存在
总存在 ,使得
,使得 成立,
成立,
所以 , 即
, 即 ,
,
即

 .
.
设 ,其中
,其中 ,则
,则 ,因而
,因而 在区间(0,1)上单调递增,
在区间(0,1)上单调递增, ,又
,又 .
.
所以 ,即
,即 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
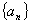 为递增数列,
为递增数列, ,
, ,则公比
,则公比 _________
_________ ,且
,且 ,现给出如下结论:
,现给出如下结论: ;②
;② ;③
;③ ;④
;④
 ,
, 在
在 上不单调,则
上不单调,则 的取值范围是__________.
的取值范围是__________. 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.

 ,
, 满足
满足 且
且 的夹角为
的夹角为 ,则
,则 .
. 则
则