Question

如图，正方体ABCD-A₁B₁C₁D₁中，M为CC₁的中点，P为平面ABCD内的动点，且A₁P和MP与平面ABCD所成的角相等，则P的轨迹为

圆

．

Answer 1

分析：连接PA，PC，根据A₁P和MP与平面ABCD所成的角相等，可得∠A₁PA=∠MPC，从而可得PA=2PC，以A为坐标原点，AB，AD分别为x，y轴，建立平面直角坐标系，设正方体的棱长为1，求出P的方程，即可得到结论．

解答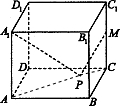：解：连接PA，PC，则∠A₁PA，∠MPC分别为A₁P和MP与平面ABCD所成的角相等
∵A₁P和MP与平面ABCD所成的角相等，
∴∠A₁PA=∠MPC
∴tan∠A₁PA=tan∠MPC
∴

AA1

PA

=

MC

PC

∵M为CC₁的中点，
∴PA=2PC
以A为坐标原点，AB，AD分别为x，y轴，建立平面直角坐标系，设正方体的棱长为1，则C（1，1）
设P（x，y），则x²+y²=4[（x-1）²+（y-1）²]
即（x-

4

3

）²+（y-

4

3

）²=

8

9

∴P的轨迹为圆
故答案为：圆．

点评：本题考查立体几何中的轨迹问题，解题的关键是确定曲线的方程，属于中档题．